Отличие простых процентов от сложных

Что такое сложный процент в инвестициях простыми словами

Знание механизма расчета по депозиту позволяет вкладчикам составить прогноз дохода. Этот расчет доступен при заключении соглашений, выполнении транзакций, перед начислением вознаграждения и капитализацией прибыли.

Банки пользуются простыми и сложными формулами.

При этом применяется фиксированная ставка, которая закрепляется договором при размещении депозита, может регулироваться в случаях:

• автоматической пролонгации договора;
• досрочного закрытия.

Плавающий тип может меняться на протяжении действия соглашения.

Изменение ставок в этом случае привязано к таким факторам:

• курсу валют;
• переводу депозита в другую категорию.

При расчете дохода учитывается ряд показателей:

• инвестиционная сумма;
• процентная ставка, ее тип;
• периодичность начислений;
• срок договора.

При использовании простой схемы расчета итог получается в результате таких математических действий. Начальная сумма умножается на годовую ставку и количество дней начисления вознаграждения и делится на количество дней по календарю и на 100.

Зачем инвестировать под сложный процент

При инвестировании денег рекомендуется выбрать оптимальный вариант, который позволит использовать преимущества сложных ставок. Вложению денег всегда предшествует планирование, анализ поставленной задачи. Капитализация прибыли от инвестирования на счет позволяет получить дополнительный доход.

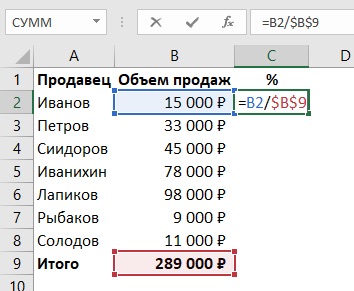
Простой расчет

Эффективной ставкой считается номинальный процент, который начисляется на сумму с капитализацией. Рассчитать доход можно в программе Excel. Для этого следует ввести исходные данные, формулы на базовый депозит, сумму с капитализацией. Действия выполняются автоматически, поэтому для получения корректного результата рекомендуется внимательно ввести информацию.

Формула

Плата за пользование средствами финансовым учреждением начисляется ежемесячно. Если вкладчик не будет снимать эти средства со счета, то они дополнят сумму основного депозита.

Формула сложного процента записывается: S=X*(1+%)n, где

• S — конечная сумма;
• X — начальный вклад;
• % — годовая ставка;
• n — количество периодов.

В результате прибыль добавляется к сумме и дает доход. Сложный расчет может действовать при открытии .

Выбирая программное предложение банка, нужно ориентироваться на итоговый доход в денежном выражении, который получится при размещении средств.

Пример

Хорошей иллюстрацией является известная евангельская притча о том, как одна бедная вдова во времена Иисуса Христа принесла в жертву в храм последнее, что у неё было — две самых мелких монеты, лепты. Если представить себе, что в то время существовали банки, и она внесла бы одну монетку в банк, то какая сумма накопилась бы на банковском счёте к сегодняшнему дню, учитывая, что банк обеспечивает капитализацию процентов в сумме, скажем, пять процентов годовых?

Последующие расчёты как раз и иллюстрируют применение сложных процентов. Для наглядности будем говорить не о лепте, а о копейке. Если ставка составляет 5 % годовых, то после первого года хранения капитал составил бы копейку плюс 5 % от неё, то есть возрос бы в (1 + 0,05) раза. На второй год 5 % рассчитывались бы уже не от одной копейки, а от величины, большей её в (1 + 0,05) раза. И, в свою очередь, данная величина увеличилась бы тоже за год в (1 + 0,05) раза. Значит, по сравнению с первичной суммой вклад за два года возрос бы в (1+,05)2{\displaystyle (1+0,05)^{2}} раз. За три года — в (1+,05)3{\displaystyle (1+0,05)^{3}} раз.

К 2020 году первичный вклад вырос бы до величины в (1+,05)2020{\displaystyle (1+0,05)^{2020}} раз больше первоначальной. Величина (1+,05)2020{\displaystyle (1+0,05)^{2020}} составляет 6,34⋅1042{\displaystyle 6,34\cdot 10^{42}}. При первоначальном вкладе в одну копейку к 2020 году сумма составит 6,34⋅1042{\displaystyle 6,34\cdot 10^{42}} рублей, то есть свыше 63 додециллионов.

Первоначальная идея применения к старинной притче оценок в сложных процентах принадлежит польскому математику Станиславу Ковалю и опубликована им в начале семидесятых годов в книге «500 математичных загадок».

Точная формула для оплаты ежемесячно

Точная формула для ежемесячного платежа

C=Pr(1−1(1+r)n){\displaystyle C=Pr/(1-1/(1+r)^{n})}

с = ежемесячный платеж
P = начальная сумма
r = ежемесячная процентная ставка
n = количество периодов выплат

Периодическое начисление

Функция суммы сложных процентов является экспоненциальной функцией с точки зрения времени.

P(t)=P(1+rn)nt{\displaystyle P(t)=P_{0}(1+{r \over n})^{nt}}

t = Общее время в годax

n = число периодов наращения в год

г = Номинальная годовая процентная ставка выражается в виде десятичной дроби. 6 т.д .:% = 0,06

nt = означает, что nt округляется до ближайшего целого числа.

Непрерывное начисление

Пределом (1+rn)nt{\displaystyle (1+{r \over n})^{nt}} при n→∞{\displaystyle n\rightarrow \infty } является ert{\displaystyle e^{rt}} (см. E (число)), таким образом, для непрерывного начисления, формула принимает вид:

P(t)=Pert{\displaystyle P(t)=P_{0}e^{rt}}

Депозитный калькулятор онлайн. Расчет процентов по депозиту.

Срисовки: мастер-класс по созданию простых и сложных рисунков своими руками с поэтапными схемами для начинающих + фото-примеры оригинальных работ

Cумма вклада

Процентная ставка (%)

Срок вклада (мес.)

Ежемесячные проценты
реинвестируютсяснимаются

Размер доходов по депозитам это один из наиболее интересных для вкладчиков вопросов.

Даже не обладая базовыми познаниями в экономике, человек со средним образованием способен подсчитать сумму, которую ему обещает выплатить коммерческий банк за пользование его деньгами.

Депозитный калькулятор онлайн

Депозит, как и достаточное количество профессиональных терминов в банковском деле, имеют итальянское происхождение, смысл которого заключается во временном хранении и использовании каких-либо материально-финансовых ценностей с целью извлечения дохода.

В современном мире такая финансовая операция, как хранение средств на депозитном счете в коммерческом банке, является наиболее консервативным инструментом финансового менеджмента, но одновременно и наиболее безопасным.

1. Составление депозитного договора
2. Открытие депозитного счета
3. Инкассирование банком средств вкладчика

Депозитный калькулятор онлайн. Расчет процентов по депозиту.

В дальнейшем все основные особенности взаимодействия между вкладчиком и банком зависят от пунктов в депозитном договоре. К таким особенностям относятся: размер и периодичность выплат клиенту по депозиту.

Обычно банк, планируя привлечения средств вкладчиков, декларирует % доходности не ниже инфляционного %. Такая политика прослеживается сейчас в большинстве экономически развитых странах (ЕС, США, Канада, Япония) у подавляющего количества кредитно-финансовых учреждениях в этих странах. Отдельные крупные финансовые холдинги, действующие в международных масштабах, анонсируют доходность по размещенным в них депозитам физических лиц на 1,5-2% инфляционного индекса (темпа роста рыночных цен, в % выражении).

Депозитный калькулятор онлайн. Рассчитайте свой доход

Если договор о привлечении средств вкладчика составлен на год, и в нем отсутствует пункт о ежемесячных выплатах клиенту, то размер таких сумм может быть вычислен клиентом, без того, чтобы им была использована опция депозитный калькулятор онлайн. Такая сервисная функция уже больше 3-4 лет точно присутствует на сайтах крупнейших российских банков, входящих в топ 100 лучших финансовых институтов в стране. Эта финансовая «программка» позволяет вкладчику рассчитать свои ежемесячные или совокупные выплаты в тех случаях, когда:

• Деньги на депозит помещаются на 2 и более лет
• Проценты по депозиту клиенту выплачиваются ежемесячно
• Процентная ставка не является фиксированной, и меняется один и более раз в период действия депозитного договора

Депозитный калькулятор онлайн, экономит и оптимизирует время

Во всех вышеперечисленных случаях для среднестатистического вкладчика осуществлять самостоятельные расчеты затруднительно. Например, в тех случаях, когда договора депозитного вклада заключается на 2 и более лет требуется знание формулы сложных процентов. А автоматизированная, присутствующая на сайте банка опция депозитный калькулятор онлайн даст возможность вкладчику произвести все подсчеты самостоятельно, и узнать свой совокупный доход по депозиту за несколько лет в течение 2-3 минут максимум.

Заполнение анкеты состоит в ответах вкладчика на три несложных вопроса:

Депозитный калькулятор онлайн, что заполнять

1. Процентная ставка по депозиту
2. Сумма депозитного вклада
3. Срок размещения средств
4. Валюту вклада

Заполнив все поля, потенциальный вкладчик нажимает по иконке «рассчитать», и в течение нескольких секунд получает итоговый результат.

Помимо удобств для клиента банка такая инновационная финансовая услуга, как депозитный калькулятор онлайн, экономит и оптимизирует время сотрудников банковских отделов работы с клиентом, давая возможность в течение рабочего дня оформлять больше договоров о привлечении средств на депозитные счета в банке.

В крупнейших российских банках можно и деньги поместить на депозит в режиме онлайн. Согласно существующей сегодня банковской статистике почти 60% доходов в структуре совокупных доходов банкам приносят депозитные вклады, и кредитное обслуживание населения является. Для российских банковских гигантов, входящих в топ 10, депозитные операции и кредиты являются основной специализацией в финансовой деятельности этих финансовых структур.

Простые и сложные проценты

Инвесторы, которые работают на рынке Форекс, сталкиваются с повторным вложением денег (реинвестированием) постоянно. Если банковские депозиты приносят владельцам прибыль через несколько месяцев или даже год, то на валютном рынке прибыль/убыток появляется после каждой сделки.

Поэтому все, кто интересуется инвестициями на Форексе, будут регулярно работать с простыми и сложными процентами. Давайте же разберемся, что же означают эти понятия.

Простой процент используется в случаях, когда база начисления процентов всегда равна начальной сумме вложений. Это могут быть специальные банковские депозиты, проценты по кредиту. Также простой процент используется, когда инвестор регулярно выводит прибыль — в каждый период времени работает первоначальная сумма.

Каждый раз, когда инвестор хочет несколько раз «прокрутить» свои деньги через инвестиционный инструмент, он сталкивается со сложным процентом. Полученная прибыль на первом круге реинвестируется и проценты уже начисляются на более крупную сумму.

В инвестициях на рынке Форекс сложный процент используется постоянно, потому что сумма вложений меняется после каждой сделки. Многие инвесторы используют тактику «вложил и забыл», оставляя полученную прибыль работать вместе со стартовым вкладом.

Разница между простыми и сложными процентами на первый взгляд кажется не такой уж большой. Но чем больше проходит времени, тем очевиднее становится преимущество сложных процентов:

Простые и сложные проценты на одном графике

Конечно, это всё теория и на практике добиться 30-кратного реинвестирования прибыли совсем непросто. Но факт остаётся фактом — сложные проценты могут сослужить хорошую службу инвестору. И чтобы умело их использовать, нужно правильно их считать, в чём помогут несколько полезных формул.

Простые проценты

На практике применяются три варианта расчета простых процентов:

• точные проценты с точным числом дней ссуды (английская практика). Обозначается как 365/365 или АТС/АТС.
• обыкновенные (коммерческие) проценты с точным числом дней ссуды (французская практика). Обозначается как 365/360 или АТС/360.
• обыкновенные проценты с приближенным числом дней ссуды (германская практика). Обозначается как 360/360.
  По схеме 360 количество дней к году принимается равным 360 (в каждом месяце по 30 дней).
  Пример. Определить приближённое число дней между 12.02.2019 и 27.08.2020.
  Если год рассматривается как промежуток, содержащий 12 месяцев продолжительностью 30 дней (дивизор равен 360 дней), то приближённое число дней рассчитывается следующим образом:
  где y — номер года, m — номер месяца в году, d — номер дня в месяце.
  n = 360*(2020-2019)+30*(8-2)+(27-12) = 555 дней

Pin

Когда срок финансовой сделки не равен целому числу лет:
S=P·(1+tT​·i)
где t — срок в днях, T — временная база (365 или 360)

Примеры задач на простые проценты

Решить

1. Ссуда в размере P = 1 млн.руб. выдана d1 = 20.01 до d2 = 05.10 включительно под i = 18% годовых. Какую сумму должен заплатить должник в конце срока при начислении простых процентов? При решении применить три метода расчёта срока ссуды.
   Начальная дата: 20.01, конечная дата: 05.10, количество дней между датами: 258
   Январь, 11 дней: с 21.01 по 31.01
   Февраль, 28 дней: с 01.02 по 28.02
   Март, 31 день: с 01.03 по 31.03
   Апрель, 30 дней: с 01.04 по 30.04
   Май, 31 день: с 01.05 по 31.05
   Июнь, 30 дней: с 01.06 по 30.06
   Июль, 31 день: с 01.07 по 31.07
   Август, 31 день: с 01.08 по 31.08
   Сентябрь, 30 дней: с 01.09 по 30.09
   Октябрь, 5 дней: с 01.10 по 05.10
   Итого: 11 + 28 + 31 + 30 + 31 + 30 + 31 + 31 + 30 + 5 = 258
   S=P·(1+tT​·i)
   1) Точные проценты с точным числом дней ссуды (365/365)
   S=1 000 000·(1+258365​·0.18)=1 127 232.88 руб.
   2) Обыкновенные проценты с точным числом дней (365/360)
   S=1 000 000·(1+258360​·0.18)=1 129 000 руб.
   3) Обыкновенные проценты с приближённым числом дней (360/360)
   Количество дней между датами: 255
   Январь, 10 дней: с 21.01 по 30.01
   Февраль, Март, Апрель, Май, Июнь, Июль, Август, Сентябрь по 30 дней
   Октябрь, 5 дней: с 01.10 по 05.10
   Итого: 10 + 30*8 + 5 = 255
   S=1 000 000·(1+255360​·0.18)=1 127 500 руб.
2. Через d = 180 дней после подписания договора должник уплатит S = 310 тыс.руб. Кредит выдан под i = 16% годовых. Какова первоначальная сумма долга при условии, что временная база равна 365 дням?
   P=S(1+tT​·i)​
   Находим современную стоимость P=310 000(1+180365​·0.16)​ = 287 328.59 руб.

Пример расчета с реальным банковским вкладом

Выше мы рассмотрели упрощенные примеры работы сложного процента. На самом деле банки используют немного усложненную формулу.

Ставка процентов представляется как

Формула универсальная и позволяет сделать вычисление для разных типов депозитов. Таким образом, наша основная формула стала чуть-чуть сложнее:

Математическое понятие «геометрическая прогрессия» помогает работать банковскому вкладу с капитализацией гораздо более эффективно, чем без капитализации. Человеческий мозг не всегда может представить разницу или она поначалу ему кажется не существенной. В действительности, на значительных отрезках времени сложный процент начинает играть огромную роль при построении капитала.

Газпромбанк Автодрайв Platinum Credit — 10 % бонусами на АЗС «Газпромнефть»

Подробнее про формулу

Банки в своей практике руководствуются несколькими формулами, позволяющими рассчитывать простые % и сложные. При их начислении применяется фиксированный и плавающий вид ставок. Фиксированную закрепляют договором при размещении вклада, она не меняется до оконца периода его действия. Она может измениться в случае автоматических пролонгаций действия договора. Также она изменится в случае досрочного разрыва соглашения между клиентом и банком с выплатой % за фактический период размещения вложений, если вклад был размещен до востребования. Эти нюансы должны быть описаны в договорах.

При каких условиях и в каком порядке будет осуществляться этот процесс, нужно описывать в договорах. Изменение процентов привязано к изменениям:

• ключевой ставки;
• валютного курса;
• переводом депозита в иную категорию и др.

Для расчетов указываются все требуемые формой данные:

• сумма вклада;
• размер % ставки конкретного вклада;
• периодичность начислений % (поквартально, помесячно, ежедневно и др.);
• срок заключения договора;
• иногда нужно знать вид применяемой ставки – она может плавать или быть зафиксированной.

Формулы сложных процентов по вкладам и примеры решения задач

Формулы сложных процентов в математике встречаются постоянно, особенно если речь идёт об экономических задачах. Представьте, что вам нужно рассчитать прибыль от банковского вклада за несколько лет. Для этого понадобится такая информация:

• начальная сумма вклада (K нулевая или К)
• ставка доходности (R) — переводится из процентов в число (10% = 0.1)
• количество периодов реинвестирования, то есть лет (n)

А конечную сумму вклада мы назовем просто K. Её можно рассчитать по формуле:

Конечная сумма при расчёте сложных процентов по вкладу

Пример задачи: Инвестор П. положил на депозит в банке 10000$ под 10% годовых. Какую прибыль он получит через 5 лет?

Для начала, давайте узнаем конечную сумму вклада по формуле:

K = 10000$ * (1 + 0.1)5 = 16105.1$

Прибыль (P) — это разница между конечной и стартовой суммой вклада. Считаем:

P = K — К = 16105.1$ — 10000$ = 6105.1$

Можно даже подсчитать прибыль в процентах, для этого нужно найти не разницу, а отношение между конечной и стартовой суммой:

P (%) = K/К — 1 = 16105.1$ / 10000$ — 1= 61.05%

Используя формулу сложных процентов, вы всегда можете предсказать результат инвестирования в будущем. Впрочем, бывают ситуации, когда вам нужно узнать не конечную, а стартовую сумму вклада. Её можно найти по той же формуле сложных процентов по вкладам, но надо немного её изменить:

Формула расчёта сложных процентов для поиска стартовой суммы вклада

Пример задачи: Инвестор В. хочет узнать, сколько ему надо вложить рублей под 20% годовых сейчас, чтобы через 3 года стать рублёвым миллионером. 

Используем формулу:

К = 1000000₽ / (1 + 0.2)3 =  578703.7₽

Кроме суммы вклада, через формулу можно найти и остальные параметры. Например, зная стартовую и конечную сумму, можно узнать процентную ставку или количество периодов реинвестирования.

Начнем с процентной ставки:

Формула расчёта сложных процентов по вкладу для поиска нужной процентной ставки

Пример задачи: Инвестор Р. хочет выяснить, вклад с какой процентной ставкой ему нужен, чтобы заработать 10000$ за 3 года, изначально вложив 20000$.

Для начала нужно посчитать конечную сумму, так как мы знаем только прибыль:

K = К+ P = 20000$ + 10000$ = 30000$

А теперь можно использовать формулу:

R = (30000$ / 20000$) ^ 1/3 — 1 = 14.47%

Чтобы получить такую доходность, банковский депозит не подойдёт, а вот консервативный ПАММ-счёт — вполне.

Напоследок давайте выясним, как рассчитать, на какой срок нужно положить деньги, чтобы получить нужную нам прибыль. Без логарифмов не обойтись:

Расчёт сложных процентов по вкладу — поиск нужного количества периодов реинвестирования

Пример задачи: сколько лет нужно держать деньги на депозите в банке под 25% годовых, чтобы 50000 рублей превратить в 100000?

Подставляем в формулу:

n = log_1+0.25 100000/50000 = 3.11 лет

Кстати, если речь идёт о банке, то 3.11 лет округляются до 4 — вы обычно не можете снять свои деньги до окончания периода действия вклада. Условия конкретного инвестиционного инструмента всегда стоит учитывать при решении подобных задач.

Кроме рассмотренных нами задач существуют и более сложные. Например, довольно распространённая история — у инвестора есть вклад с возможностью пополнения. Часть каждой зарплаты отправляется туда и надо выяснить, какой же будет результат по итогам.

Пример задачи: Инвестор З. вложил 1000$ и откладывает 50$ каждый месяц. Процентная ставка — 1% в месяц. Какая сумма накопится через 5 лет?

Чтобы узнать результат, нужно создать табличку:

Расчёт результатов инвестирования с доливками, с учётом сложных процентов

В первый месяц сумма инвестиций составила 1000$, на неё начислен 1% — итого 1010$. Во второй месяц работают уже 1010$ и еще 50$, которые инвестор внёс дополнительно. Итого — 1070.10. И так далее…

Разумеется, считать эти таблички каждый раз — довольно напряжно, решать логарифмы — тем более. Поэтому специально для вас при помощи программы Microsoft Excel я сделал небольшой файлик для решения задач по сложным процентам.

Формула простых процентов.

Она используется тогда, когда начисляемый доход присоединяется к основному телу депозита в конце его срока или не присоединяется и выводится на текущий счет или пластиковую карточку. Этот порядок расчета стоит учесть, когда размещается солидная сумма на длительный срок. Обычно в данном случае банки применяют варианты размещения без капитализации, что понижает общую выгоду вкладчика.

Формула простого %:
Сумма % — это  доход, полученный через i-ый промежуток времени.

Р – изначальный объем вложений.

i – депозитная годовая ставка.

t – срок вложения.

T – число дней в году.

Рассмотрим пример: разместим 100 000 рублей на полгода под 12%. Рассчитаем полученный доход:

Таким образом, через полгода со счета можно будет снять 105 950,68 руб.

Как поможет сложный процент в построении капитала?

Самый впечатляющий пример работы сложного процента будет ниже.

Представьте, что базовая сумма у вас совсем мизерная — 1000 рублей. Но вы каждый месяц можете откладывать от зарплаты по 1000 рублей.

Теперь прикинем варианты, какие проценты дают доступные средства сохранения и инвестирования денег в год:

• 5% — государственные облигации, так называемые облигации федерального займа. Это упрощенно, на самом деле суммы может быть побольше.
• 10% — самый щедрый банковский вклад
• 15% — смешанный инвестиционный портфель акций и облигаций
• 20% — такой процент годовых может дать портфель из акций фондовой биржи.

Давайте не будем больше приводить формулы, так как мы уже все подробно рассказали. Теперь просто возьмем итоговые цифры, которые поражают воображение неподготовленного человека.

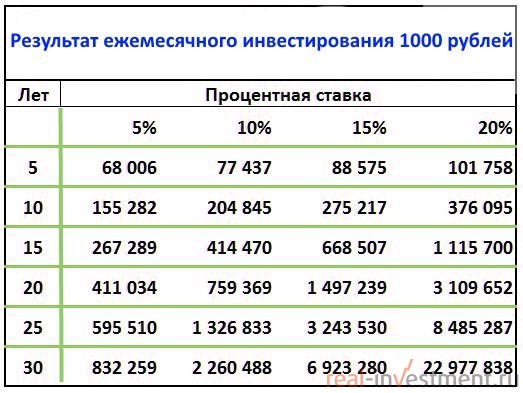
Как мы видим результаты впечатляющие, суммы растут как снежный ком. Вы все можете проверить по калькулятору или экселю, здесь нет обмана. Вы действительно можете стать миллионером, откладывая всего по 1000 рублей в месяц.

А что если вы сможете откладывать по 10000 рублей? Теперь подрисуйте в таблице везде по нолику и еще раз удивитесь результатам.

Почему в акции инвестировать безопасно? Почему акции непременно будут расти на 20% годовых? Подробная информация о стратегии и ответы на эти вопросы вы получите на нашем вебинаре об индексном инвестировании, а точнее записи этого вебинара.

Вычисление эффективной процентной ставки депозита в банке

Как зарегистрироваться и войти

Статьи о кредитах

Фиксированная или плавающая процентная ставка?

Кредитование: типы кредитов

Автокредит без справки о доходах

Ставка рефинансирования

Что такое сложный процент?

Сложным процентом называют геометрическую прогрессию денежной суммы, при которой начисленные проценты прибыли прибавляются к базовой сумме, в следующем периоде базовая сумма увеличивается и процент начисляется уже на нее. За счет этого эффекта доходность получается выше, чем при простом проценте.

Капитализация или реинвестирование — это суммирование начисляемых процентов с базовой суммой в обозначенный период. В последующем периоде базовая сумма изменяется на эту величину процента, таким образом достигается прогрессивное или лавинообразное увеличение суммы средств. При подсчете по формуле простого процента, базовая сумма всегда остается неизменной.

Вся эта теория для неподготовленного читателя кажется через чур трудоемкой и запутанной. Но мы вас уверяем, ничего сверхсложного в формуле сложного процента и его отличия от простого нет. Сейчас разберем несколько задач и все встанет на свои места.

Параметры кредита

• Требования к заемщику
• Документы
• Обеспечение и страхование
• Дополнительно

Минимальный возраст на момент получения кредита	21 год
Гражданство	Требуется
Регистрация	Постоянная в любом регионе присутствия банка
Стаж работы на последнем месте	Не менее 3 месяцев
Мобильный телефон	Требуется
Рабочий телефон	Требуется
Другие ограничения	Постоянный доход от 10 000 рублей после вычета налогов

Калькулятор сложных процентов от Вебинвеста

Многие формулы сложных процентов в математике на обычном калькуляторе не посчитаешь — нужно использовать специальные программы или сайты. Microsoft Excel позволяет делать практически любые прикладные расчёты быстро и удобно — всего-то нужно скачать файл и работать с ним.

По формулам из статьи я сделал небольшой калькулятор для расчёта сложных процентов. Вот так выглядит одна из страниц:

Скриншот из калькулятора сложных процентов с капитализацией. 

С помощью файла вы сможете решить задачи, которые мы рассматривали по ходу статьи:

• расчёт конечной суммы вклада;
• расчёт начальной суммы вклада;
• расчёт нужной процентной ставки;
• расчёт срока инвестирования;
• расчёт конечной суммы вклада с учётом добавочных вложений или снятия прибыли.

Как получить калькулятор сложных процентов от Вебинвеста? Очень легко — воспользуйтесь формой ниже:

Больше подробностей о калькуляторе сложных процентов вы можете узнать на этой странице.

Ну что, ощутили магию сложных процентов? Если да, поделитесь статьёй в соцсетях, пусть ваши друзья тоже её почувствуют 🙂

Удачи и терпения в инвестициях!

Как воспользоваться сложным процентом?

Стоит сразу поставить точки над i и уточнить, что принцип сложного процента касается не только инвестиций. Это общая формула, которую можно применить к работе, учебе, личным отношениям, да чему угодно. Подумайте сами, когда человек годами занимается определенным делом, отдаваясь ему на все сто – он планомерно и стабильно увеличивает свой опыт. Конечно, и возрастные изменения дадут о себе знать. Но, скажем так, с тренировками и упорным трудом, каждый может добиться значимого результата.

Личное развитие

Касательно языков. Учите по три слова в день, и через год Ваш словарный запас перевалит за 1000 слов. Особо актуально в канун Нового Года. Более того, регулярная практика вынудит Вас познавать и азы грамматики, строения лексики, функционированию языка и так далее. Иными словами, узкий аспект широкого поля действия не только позволит совершенствоваться исключительно в этой парадигме, но и расширять и углублять свои познания как личности.

Другой пример – регулярные физические тренировки. Нет разницы: силовые, кардио, кроссфит. По мере развития Ваших физических навыков, будут расти и когнитивные возможности. Мозг будет чаще омываться кровью, богатой кислородом, и лучше работать. Кстати, именно это и послужило развенчанию мифа про «тупых спортсменов».

И наоборот. Все гении, которые выходили на Нобелевские премии, признавали необходимость физических нагрузок. Все потому, что и научный труд, и физический, и стремление приумножить капитал в инвестировании стоят на системном принципе.

Инвестирование и сложный процент

Здесь речь идет о заработке и деньги – это основной механизм, в котором Вы можете протестировать теорию сложного процента. Всё, что Вам понадобится, это:

• Выбрать интересный для Вас тариф. Помните, чем выше будет сумма инвестиции – тем быстрее вы сможете выйти на полноценный пассивный доход;
• Приобрести его, и воспользоваться сопутствующими гарантиями для сохранности права на прибыль и защиты Вашего актива;
• Сохранять процентные выплаты.

На счет последнего пункта. Стратегия инвестирования позволяет как держать крупную сумму в постоянном обороте, так и снимать некий процент, тем самым поощряя себя, но и увеличивая грядущую прибыль. Подумайте сами, что более приоритетно для Вас сейчас? Получить немного денег, или стать полностью финансово независимым через год-два-три?

Если Вы достаточно независимы, воспользуйтесь этим инвестиционным механизмом.

Формула сложного процента

Формула сложного процента позволяет быстро и просто посчитать любую задачу на вклады. Выглядит эта формула так:

$S=X*(1+m)^{n}$, где

S – итоговая сумма вклада

Х – начальная сумма вклада

m-процент в виде десятичной дроби

n-количество периодов, за которые планируется получит прибыль.

Обратите внимание, что периоды могут быть месяцами, годами, неделями, кварталами и т.д. Это нужно учитывать при решении задач на сложный процент

Теперь подсчитаем, какую прибыль получит Петя за 10 лет.

X=10000

m=0,1

n=10

Подставим все в формулу:

$S=10000*{(1+0,1)^{10}}=25937 руб$ – результат округлен до целых чисел.

В процессе вычисления без калькулятора не обойтись, зато все расчеты производятся в два-три действия. Иногда по требованию учителя или составителя учебника, округление придется производить до сотых.

Что мы узнали?

Мы поговорили о том, что такое процент. Разобрались с определением сложного процента и привели формулу сложного процента. Привели небольшой пример сложного процента, результат которого нашли с помощью формулы.

1. Вопрос 1 из 5

Начать тест(новая вкладка)

Формула расчёта сложного процента для разных периодов

Помимо стандартного вида капитализации, когда проценты начисляются раз в год, существует и более выгодный вид капитализации. Речь идёт о ежемесячных начислениях процентов и с последующим ростом общей прибыли.

Единственным отличием от основной формулы является, тот факт, что n это уже не количество лет, а количество месяцев. Также показатель процентов стоит разделить на 12 месяцев, чтобы получить точные месячные данные.

Если бы данная формула использовалась для полугодового расчёта, то процентный показатель стоило бы разделить на 2 ( так как 2 полугодия в году), а n обозначало бы количество полугодий. Подобный принцип будет и для расчётов за квартал.

Сложные проценты способны вас обеспечить прибылью гораздо лучше чем простые проценты. Однако стоит заметить, что прибыль здесь будет формироваться на долгосрочной основе. Чтобы вы наглядно поняли разницу между этими процентами и оценили выгоду для себя, рассмотрим два небольших сравнительных примера.

Представьте, что вы инвестировали 1 000 000 рублей на 12 лет под 10 % годовых. Вы не осуществляете дополнительных взносов к вкладу, а прибыль снимаете.

Во втором случае условия остаются таким же, только с разницей, что вы прибыль не снимаете и она суммируется к основному вкладу и уже прибыль рассчитывается от новой суммы с каждым годом. Для наглядности сделаем расчёты в цифрах.

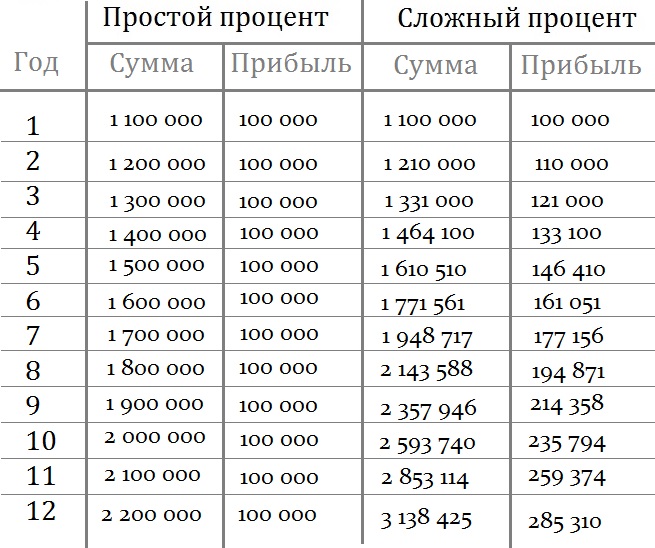
Как видите, отличие значительное. Важным моментом здесь будет являться, тот факт, что чем чаще буду начисляться проценты, чем выше ваша ожидаемая доходность. При одинаковой процентной ставке начисление по сложным процентам, намного выгоднее, чем по простым.

Часто бывает так, что перед человеком стоит нелёгкая задача, выбрать вклад с более простым начислением процентов, но с большой процентной ставкой, либо выбрать вклад с меньшей процентной ставкой, но с возможностью капитализацией этих самых процентов.

Перед выбором внимательно изучите договор, который предоставляется банком. Также оцените ваши цели и задачи, чтобы лучше понять, что вам больше подходит.

Не стоит забывать, что проценты способны приносить выгоду лишь до определённого периода времени либо после определённого периода

 Немаловажное значение играет время

Ведь капитализация процентов способна принести ощутимую выгоду и пользу не всем, а лишь тем, кто собирается осуществить вложения на более длительный срок, как правило, от 5 лет и более.  Вся прелесть капитализации процентов в том, что чем дольше лежит вклад, тем на большую доходность можно претендовать.

Также, банком в договорах могут указываться разные условия, например, если вкладчик ранее чем через 10 лет снимет прибыль со своего вклада, то это может привести к значительному понижению его дохода, а может и к полной утрате дохода в будущем.

Понимание, того как работают сложные проценты вам поможет больше заработать на своих капиталовложениях. Практически любой банкир вам скажет, что вклад по более низкой ставке но с возможностью капитализации, более выгоден, чем вклад с более высокой ставкой, но без возможности сложного начисления процентов.

Как даже с 1 000 рублей в кармане создать пассивный доход к пенсии

Пенсионный возраст увеличили, накопительную пенсию заморозили, регулярно проводят пенсионную реформу и меняют условия. Все эти хаотичные телодвижения говорят только о том, что у руководства нет четкого плана действий и видения, как же должна начисляться пенсия в нашей стране.

Какой вывод простому гражданину нужно сделать из всего этого? Только один – накопить на пенсию самостоятельно. И поможет в этом сложный процент. На конкретных расчетах посмотрим, как даже с 1 000 ₽ в месяц создать пассивный доход. Но для начала замечательная сказка из книги Бодо Шефера “Мани, или Азбука денег”.

Жил-был когда-то крестьянин. Каждое утро он ходил в курятник, чтобы взять на завтрак яйцо, которое снесла его курица. Но однажды он нашел в гнезде не обычное яйцо, а золотое. Сначала он не мог в это поверить. Возможно, кто-то решил над ним зло подшутить. Но ювелир, которому он принес показать яйцо, подтвердил, что оно из чистого золота. Крестьянин выгодно продал яйцо и устроил большой праздник.

На следующее утро он пошел в курятник раньше, чем обычно. В гнезде опять лежало золотое яйцо. Так продолжалось несколько дней. Но крестьянин был жадным и хотел побыстрее разбогатеть. Он злился на свою курицу, потому что “глупая птица” не могла объяснить ему, как она умудряется нести золотые яйца. Ему казалось, что тогда он мог бы и сам нести золотые яйца. Тогда у него было бы каждый день по два яйца. И однажды крестьянин так сильно разозлился, что вбежал в курятник и зарезал свою курицу. Некому стало нести золотые яйца.

Мораль этой сказки такова: нельзя резать курицу, несущую золотые яйца. Но чтобы получать золотые яйца, надо сначала завести курочку. Этим вы и должны заняться как можно скорее. Время – друг инвестора и враг того, кто откладывает на потом создание личного капитала.

Пример 1. Необходимо рассчитать, сколько денег нужно накопить, чтобы жить на пассивный доход через какое-то количество лет. Допустим, мы хотим на пенсии ежемесячно получать 50 000 ₽. Учтем инфляцию 4 %.

Ставку доходности примем равной 10 %. Ее размер зависит от состава инвестпортфеля. Если решили копить в облигациях, то закладывать надо меньший %. Если составить сбалансированный портфель из разных инструментов (например, ETF, акции и облигации отдельных эмитентов, золото), то 10 % – очень консервативная оценка. На практике получается значительно больше.

Расчет без учета инфляции: 50 000 * 12 месяцев / 0,1 = 6 000 000 ₽. Для учета инфляции воспользуемся онлайн-калькулятором. Необходимо накопить уже 10 000 000 ₽.

Пример 2. Есть начальный капитал 50 000 ₽ с ежемесячным вложением равной суммы: 1 000 ₽, 5 000 ₽ и 10 000 ₽. Доходность – 10 %, примем ежегодное начисление %. Сколько накопим через 10, 20, 30 и 40 лет?

Сумма ежемесячных взносов	Срок накопления
10 лет	20 лет	30 лет	40 лет
1 000 ₽	320936,22	1023674,99	2846398,39	7574073,45
5 000 ₽	1085932,6	3772874,97	10742111,47	28818516,12
10 000 ₽	2042178,08	7209374,94	20611752,84	55374069,46

Какие выводы мы можем сделать из этих расчетов:

1. Накопить на пассивный доход в 50 000 ₽ в месяц мы сможем, откладывая 5 000 ₽ в течение 30 лет. Если инвестируем по 10 000 ₽, то уже примерно через 23 года можно выходить на пенсию.
2. С ежемесячными 1 000 ₽ нужно довольствоваться меньшей суммой пассивного дохода. Например, чтобы получать ежемесячно 35 000 ₽, надо накопить 7 000 000 ₽. Из таблицы видно, что только через 40 лет достигнем этого. А вот для ежемесячной прибавки к пенсии в 20 000 ₽ понадобится накопить 4 000 000 ₽ за 35 лет.

Поиграйте своими цифрами в любом финансовом калькуляторе сложных процентов. У кого-то начальная или ежемесячная сумма будет больше, кто-то рассмотрит меньший или больший срок и т. д.

Вспомогательные формулы

Привожу еще пару вспомогательных формул, которые могут пригодиться при составлении личного финансового плана. Они выражаются из уже написанных выше. Рассмотрим все на примерах задач.

Задача №1

Дано:

• у вас есть 60 тыс. рублей
• вы хотите приумножить их до 250 тыс. рублей
• у вас есть срок 15 лет

Найти:

под какую процентную ставку нужно вложить деньги?

Расчет:

Ответ равен 10,03 процентам

Задача №2

Дано:

• у вас есть 50 тыс. рублей
• вы хотите приумножить их до 1 млн. рублей
• вы уверены, что сможете вложить их под 40% годовых

Найти:

сколько потребуется для этого времени в годах?

Расчет:

Ответ: 8,9 лет.