Матрицы и массивы numpy в python
Содержание:
- Введение в Numpy
- 3.4. Суммы, разности, произведения
- Пакеты в SciPy
- Функции обработки сигналов
- Полиномы (numpy.polynomial)¶
- Контроль доступа к атрибутам
- Как создаются матрицы в Python?
- Навигация по записям
- Менеджеры контекста
- Транспонирование и изменение формы матриц в numpy
- Заполнение матрицы значениями с клавиатуры
- Создание векторов и матриц
- Работа с массивами с заданным размером в Python
- Представление своих классов
- Ввод списка (массива) в языке Питон
- Решение системы линейных уравнений
- Интегральные функции
- 7.3. Статистика
- Обработка текста в NumPy на примерах
- Копирование
- Tricks and Tips¶
- Runtastic
- Функции (методы) для расчета статистик в Numpy
- Примеры работы с NumPy
- 7.4. Генерация случайных значений
Введение в Numpy
Константы и функции numpy
| np.pi | Число pi |
| np.e | Число e |
| np.cos | Косинус |
| np.sin | Синус |
| np.tan | Тангенс |
| np.acos | Арккосинус |
| np.asin | Арксинус |
| np.atan | Арктангенс |
| np.exp | Экспонента |
| np.log | Логарифм натуральный |
| np.log2 | Логарифм по основанию 2 |
| np.log10 | Логарифм десятичный |
| np.sqrt | x1/2 |
| np.add, np.subtract, np.multiply, np.divide | +, -, *, / |
| np.power(a, b) | a**b |
| np.remainder(a, b) | остаток от деления a%b |
| np.reciprocal(a) | 1/a |
| np.real, np.imag, np.conj | действительная часть; мнимая часть; a+bj заменяется на a-bj |
| np.sign | знак, 1, -1 или 0 |
| np.abs | модуль |
| np.floor, np.ceil, np.rint | преобразуем к целым числам |
| np.round | округление с указанной точностью |
Агрегации
| np.mean | среднее |
| np.std | стандартное отклонение |
| np.var | дисперсия |
| np.sum | сумма всех элементов |
| np.prod | произведение всех элементов |
| np.cumsum | сумма всех элементов по указанной оси |
| np.cumprod | произведение всех элементов по указанной оси |
| np.min, np.max | минимальное и максимальное число в массиве |
| np.argmin, np.argmax | индекс минимального и максимального числа в массиве |
| np.all | True если все элементы в массиве НЕ 0 |
| np.any | True если хоть один элемент в массиве не 0 |
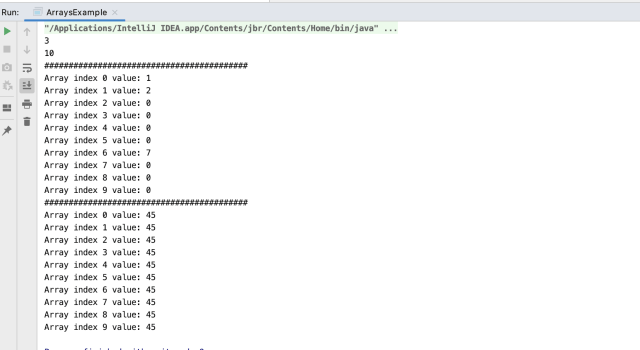
In : data = np.arange(1,10).reshape(3,3)
In : data
Out: array(,
,
])
In : data.sum()
Out: 45
In : data.sum(axis=0)
Out: array()
In : data.sum(axis=1)
Out: array()
sort — сортировка массива
>>> a = np.array(,])
>>> np.sort(a)
array(,
])
>>> np.sort(a, axis=)
array()
>>> np.sort(a, axis=0)
array(,
])
Сравнение массивов
>>> a == b
array(,
], dtype=bool)
>>> a < 2
array(, dtype=bool)
>>> np.array_equal(a, b)
In : a = np.array()
In : b = np.array()
In : a < b
Out: array(, dtype=bool)
In : np.all(a < b)
Out: False
In : np.any(a < b)
Out: True
In : np.all(a < b):
...: ("All elements a are smaller than their corresponding element b")
...: np.any(a < b):
...: ("Some elements a are smaller than their corresponding elemment b")
...: :
...: ("All elements b are smaller than their corresponding element a")
Some elements a are smaller than their corresponding elemment b
Как заставить свою функцию работать с векторами
In : heaviside(x):
...: 1 x > 0 0
In : heaviside(-1)
Out: 0
In : heaviside(1.5)
Out: 1
In : x = np.linspace(-5, 5, 11)
In : heaviside(x)
...
: The truth value of an array with more than one element ambiguous. Use a.any()
a.all()
In : vheaviside = np.vectorize(heaviside)
In : vheaviside(x)
Out: array()
3.4. Суммы, разности, произведения
- Произведение элементов массива по заданной оси.
- Сумма элементов массива по заданной оси.
- Произведение элементов массива по заданной оси в котором элементы NaN учитываются как 1.
- Сумма элементов массива по заданной оси в котором элементы NaN учитываются как 0.
- Возвращает накопление произведения элементов по заданной оси, т.е. массив в котором каждый элемент является произведением предшествующих ему элементов по заданной оси в исходном массиве.
- Возвращает накопление суммы элементов по заданной оси, т.е. массив в котором каждый элемент является суммой предшествующих ему элементов по заданной оси в исходном массиве.
- Возвращает накопление произведения элементов по заданной оси, т.е. массив в котором каждый элемент является произведением предшествующих ему элементов по заданной оси в исходном массиве. Элементы NaN в исходном массиве при произведении учитываются как 1.
- Возвращает накопление суммы элементов по заданной оси, т.е. массив в котором каждый элемент является суммой предшествующих ему элементов по заданной оси в исходном массиве. Элементы NaN в исходном массиве при суммировании учитываются как 0.
- Возвращает n-ю разность вдоль указанной оси.
- Разность между последовательными элементами массива.
- Дискретный градиент (конечные разности вдоль осей) массива .
- Векторное произведение двух векторов.
- Интегрирование массива вдоль указанной оси методом трапеций.
Пакеты в SciPy
В SciPy есть набор пакетов для разных научных вычислений:
| Название | Описание |
|---|---|
| Алгоритмы кластерного анализа | |
| Физические и математические константы | |
| Быстрое преобразование Фурье | |
| Решения интегральных и обычных дифференциальных уравнений | |
| Интерполяция и сглаживание сплайнов | |
| Ввод и вывод | |
| Линейная алгебра | |
| N-размерная обработка изображений | |
| Метод ортогональных расстояний | |
| Оптимизация и численное решение уравнений | |
| Обработка сигналов | |
| Разреженные матрицы | |
| Разреженные и алгоритмы | |
| Специальные функции | |
| Статистические распределения и функции |
Подробное описание можно найти в официальной документации.
Эти пакеты нужно импортировать для использования библиотеки. Например:
Прежде чем рассматривать каждую функцию в подробностях, разберемся с теми из них, которые являются одинаковыми в NumPy и SciPy.
Функции обработки сигналов
Обработка сигналов — это область анализа, модификации и синтеза сигналов: звуков, изображений и т. д. SciPy предоставляет некоторые функции, с помощью которых можно проектировать, фильтровать и интерполировать одномерные и двумерные данные.
Фильтрация:
Фильтруя сигнал, можно удалить нежелаемые составляющие. Для выполнения упорядоченной фильтрации используется функция . Она выполняет операцию на массиве. Синтаксис следующий:
— N-мерный массив с входящими данными
— массив масок с тем же количеством размерностей, что и у массива
— неотрицательное число, которое выбирает элементы из отсортированного списка (0, 1…)
Пример:
Вывод:
Сигналы
Подпакет также состоит из функций, с помощью которых можно генерировать сигналы. Одна из таких — . Она является генератором частотно-модулированного сигнала, а ее синтаксис следующий:
Пример:
Вывод:
Полиномы (numpy.polynomial)¶
Модуль полиномов обеспечивает стандартные функции работы с полиномами разного вида. В нем реализованы полиномы
Чебышева, Лежандра, Эрмита, Лагерра. Для полиномов определены стандартные арифметические функции ‘+’, ‘-‘, ‘*’, ‘//’,
деление по модулю, деление с остатком, возведение в степень и вычисление значения полинома
Важно задавать область
определения, т.к. часто свойства полинома (например при интерполяции) сохраняются только на определенном интервале.
В зависимости от класса полинома, сохраняются коэффициенты разложения по полиномам определенного типа, что позволяет
получать разложение функций в ряд по полиномам разного типа
| Типы полиномов | Описание |
|---|---|
| Polynomial(coef) | разложение по степеням «x» |
| Chebyshev(coef) | разложение по полиномам Чебышева |
| Legendre(coef) | разложение по полиномам Лежандра |
| Hermite(coef) | разложение по полиномам Эрмита |
| HermiteE(coef) | разложение по полиномам Эрмита_Е |
| Laguerre(coef) | разложение по полиномам Лагерра |
- coef – массив коэффициентов в порядке увеличения
- domain – область определения проецируется на окно
- window – окно. Сдвигается и масштабируется до размера области определения
Некоторые функции (например интерполяция данных) возвращают объект типа полином. У этого объекта есть набор методов,
позволяющих извлекать и преобразовывать данные.
| Методы полиномов | Описание |
|---|---|
| __call__(z) | полином можно вызвать как функцию |
| convert() | конвертирует в полином другого типа, с другим окном и т.д |
| copy() | возвращает копию |
| cutdeg(deg) | обрезает полином до нужной степени |
| degree() | возвращает степень полинома |
| deriv() | вычисляет производную порядка m |
| fit(x, y, deg) | формирует полиномиальную интерполяцию степени deg для данных (x,y) по методу наименьших квадратов |
| fromroots(roots) | формирует полином по заданным корням |
| has_samecoef(p) | проверка на равенство коэффициентов. |
| has_samedomain(p) | проверка на равенство области определения |
| has_samewindow(p) | проверка на равенство окна |
| integ() | интегрирование |
| linspace() | возвращает x,y — значения на равномерной сетке по области определения |
| mapparms() | возвращает коэффициенты масштабирования |
| roots() | список корней |
| trim() | создает полином с коэффициентами большими tol |
| truncate(size) | ограничивает ряд по количеству коеффициентов |
- p – полином
- x, y – набор данных для аппроксимации
- deg – степень полинома
- domain – область определения
- rcond – относительное число обусловленности элементы матрицы интерполяции с собственными значениями меньшими данного будут отброшены.
- full – выдавать дополнительную информацию о качестве полинома
- w – веса точек
- window – окно
- roots – набор корней
- m – порядок производной (интеграла)
- k – константы интегрирования
- lbnd – нижняя граница интервала интегрирования
- n – число точек разбиения
- size – число ненулевых коэффициентов
Контроль доступа к атрибутам
Вы можете определить поведение для случая, когда пользователь пытается обратиться к атрибуту, который не существует (совсем или пока ещё). Это может быть полезным для перехвата и перенаправления частых опечаток, предупреждения об использовании устаревших атрибутов (вы можете всё-равно вычислить и вернуть этот атрибут, если хотите), или хитро возвращать , когда это вам нужно. Правда, этот метод вызывается только когда пытаются получить доступ к несуществующему атрибуту, поэтому это не очень хорошее решение для инкапсуляции.
В отличии от , решение для инкапсуляции. Этот метод позволяет вам определить поведение для присвоения значения атрибуту, независимо от того существует атрибут или нет. То есть, вы можете определить любые правила для любых изменений значения атрибутов. Впрочем, вы должны быть осторожны с тем, как использовать , смотрите пример нехорошего случая в конце этого списка.
Это то же, что и , но для удаления атрибутов, вместо установки значений
Здесь требуются те же меры предосторожности, что и в чтобы избежать бесконечной рекурсии (вызов в определении вызовет бесконечную рекурсию).
выглядит к месту среди своих коллег и , но я бы не рекомендовал вам его использовать. может использоваться только с классами нового типа (в новых версиях Питона все классы нового типа, а в старых версиях вы можете получить такой класс унаследовавшись от )
Этот метод позволяет вам определить поведение для каждого случая доступа к атрибутам (а не только к несуществующим, как ). Он страдает от таких же проблем с бесконечной рекурсией, как и его коллеги (на этот раз вы можете вызывать у базового класса, чтобы их предотвратить). Он, так же, главным образом устраняет необходимость в , который в случае реализации может быть вызван только явным образом или в случае генерации исключения . Вы конечно можете использовать этот метод (в конце концов, это ваш выбор), но я бы не рекомендовал, потому что случаев, когда он действительно полезен очень мало (намного реже нужно переопределять поведение при получении, а не при установке значения) и реализовать его без возможных ошибок очень сложно.
Как создаются матрицы в Python?
Добавление и модификация массивов или матриц (matrix) в Python осуществляется с помощью библиотеки NumPy. Вы можете создать таким образом и одномерный, и двумерный, и многомерный массив. Библиотека обладает широким набором пакетов, которые необходимы, чтобы успешно решать различные математические задачи. Она не только поддерживает создание двумерных и многомерных массивов, но обеспечивает работу однородных многомерных матриц.
Чтобы получить доступ и начать использовать функции данного пакета, его импортируют:
import numpy as np
Функция array() — один из самых простых способов, позволяющих динамически задать одно- и двумерный массив в Python. Она создаёт объект типа ndarray:
array = np.array(/* множество элементов */)
Для проверки используется функция array.type() — принимает в качестве аргумента имя массива, который был создан.
Если хотите сделать переопределение типа массива, используйте на стадии создания dtype=np.complex:
array2 = np.array([ /*элементы*/, dtype=np.complex)
Когда стоит задача задать одномерный или двумерный массив определённой длины в Python, и его значения на данном этапе неизвестны, происходит его заполнение нулями функцией zeros(). Кроме того, можно получить матрицу из единиц через функцию ones(). При этом в качестве аргументов принимают число элементов и число вложенных массивов внутри:
np.zeros(2, 2, 2)
К примеру, так в Python происходит задание двух массивов внутри, которые по длине имеют два элемента:
array(] ]] )
Если хотите вывести одно- либо двумерный массив на экран, вам поможет функция print(). Учтите, что если матрица слишком велика для печати, NumPy скроет центральную часть и выведет лишь крайние значения. Дабы увидеть массив полностью, используется функция set_printoptions(). При этом по умолчанию выводятся не все элементы, а происходит вывод только первой тысячи. И это значение массива указывается в качестве аргумента с ключевым словом threshold.
Навигация по записям
Менеджеры контекста
PEP 343
-
Определяет, что должен сделать менеджер контекста в начале блока, созданного оператором . Заметьте, что возвращаемое значение и есть то значение, с которым производится работа внутри .
-
Определяет действия менеджера контекста после того, как блок будет выполнен (или прерван во время работы). Может использоваться для контроллирования исключений, чистки, любых действий которые должны быть выполнены незамедлительно после блока внутри with. Если блок выполнен успешно, , , и будут установлены в . В другом случае вы сами выбираете, перехватывать ли исключение или предоставить это пользователю; если вы решили перехватить исключение, убедитесь, что возвращает после того как всё сказано и сделано. Если вы не хотите, чтобы исключение было перехвачено менеджером контекста, просто позвольте ему случиться.
contextlib
Транспонирование и изменение формы матриц в numpy
Нередки случаи, когда нужно повернуть матрицу. Это может потребоваться при вычислении скалярного произведения двух матриц. Тогда возникает необходимость наличия совпадающих размерностей. У массивов NumPy есть полезное свойство под названием , что отвечает за транспонирование матрицы.
Некоторые более сложные ситуации требуют возможности переключения между размерностями рассматриваемой матрицы. Это типично для приложений с машинным обучением, где некая модель может запросить определенную форму вывода, которая является отличной от формы начального набора данных. В таких ситуациях пригодится метод из NumPy. Здесь от вас требуется только передать новые размерности для матрицы. Для размерности вы можете передать , и NumPy выведет ее верное значение, опираясь на данные рассматриваемой матрицы:
Еще больше размерностей NumPy
NumPy может произвести все вышеперечисленные операции для любого количества размерностей. Структура данных, расположенных центрально, называется , или n-мерным массивом.
В большинстве случаев для указания новой размерности требуется просто добавить запятую к параметрам функции NumPy:
Shell
array(,
,
],
,
,
],
,
,
],
,
,
]])
|
1 |
array(1.,1., 1.,1., 1.,1., 1.,1., 1.,1., 1.,1., 1.,1., 1.,1., 1.,1., 1.,1., 1.,1., 1.,1.) |
Заполнение матрицы значениями с клавиатуры
Пусть программа получает на вход двумерный массив, в виде строк, каждая из которых содержит чисел, разделенных пробелами. Как их считать? Например, так:
A = []
for i in range(n):
A.append(list(map(int, input().split()))) #метод list() создает список(массив) из набора данных, указанных в скобках
Или, без использования сложных вложенных вызовов функций:
A = []
for i in range(n):
row = input().split() # считали строку с числами, разбили на элементы по пробелам (получили массив row)
for i in range(len(row)):
row = int(row) # каждый элемента списка row преобразовали в число
A.append(row) # добавили массив row к массиву A
Создание векторов и матриц
Вектора и матрицы – это основные объекты, которыми приходится оперировать в машинном обучении. Numpy предоставляет довольно много удобных функций, которые строят эти объекты.
Перед тем как их использовать не забудьте импортировать Numpy в проект.
>>>import numpy as np
np.arange()
Функция arange() аналогична по своему назначению функции range() из стандартной библиотеки Python. Ее основное отличие заключается в том, что arange() позволяет строить вектор с указанием шага в виде десятичной дроби.
Синтаксис использования функции следующий:
arange(stop)
arange(start, stop)
arange(start, stop, step)
В первом варианте будет создан вектор из целых чисел от 0 до stop.
>>> np.arange(10) array()
Второй вариант позволяет задавать интервал, в этом случае вектор также будет содержать целые числа.
>>> np.arange(5, 12) array()
Третий вариант позволяет определить интервал чисел и шаг, который может быть десятичным числом
>>> np.arange(1, 5, 0.5) array()
np.matrix()
Matrix является удобным инструментом для задания матрицы. При этом можно использовать Matlab стиль, либо передать в качестве аргумента список Python (или массив Numpy).
Вариант со списком Python.
>>> a = , ] >>> np.matrix(a) matrix(, ])
Вариант с массивом Numpy.
>>> b = np.array(, ]) >>> np.matrix(b) matrix(, ])
Вариант в Matlab стиле.
>>> np.matrix('')
matrix(,
])
np.zeros(), np.eye()
В арсенале Numpy есть функции для создания специальных матриц: нулевых и единичных. Нулевой называется матрица, состоящая полностью из нулей. Для ее создания удобно использовать функцию zeros(), в качестве аргумента в нее передается кортеж из двух элементов, первый из них – это количество строк, второй – столбцов.
>>> np.zeros((3, 4)) array(, , ])
Функция eye() создает единичную матрицу – квадратную матрицу, у которой элементы главной диагонали равны единицы, все остальные – нулю.
>>> np.eye(3) array(, , ])
Работа с массивами с заданным размером в Python
Объявление массива в Python известного размера
Массив с определенным числом элементов N в Python объявляется так, при этом всем элементам массива присваивается нулевое значениеНазвание массива = *NЗадание значений элементов массива в python.
Задать значение элементов массива можно при объявлении массива. Это делается такНазвание массива =
Название массива = значение элемента
При этом массив будет иметь фиксированный размер согласно количеству элементов.
Пример. Задание значений элементов массива в Python двумя способами.
Способ №1.a =
Способ №2.a = 0
a = 1
a = 2
a = 3
a = 4
Таблица основных типов данных в Python.
При работе с массивами удобно использовать цикл for для перебора всех элементов массива.a = * размер массива
for i in range(размер массива):
a = выражение
Размер массива в Питон можно узнать с помощью команды len(имя массива)
Пример программы на Python, которая вводит массив с клавиатуры, обрабатывает элементы и выводит на экран измененный массив С клавиатуры вводятся все элементы массива, значения элементов увеличиваются в два раза. Выводим все значения элементов в консоль. Чтобы элементы массива выводились в одну строку через пробел, используем параметр end =» » в операторе вывода на экран print(a, end = » «)a = * 4
for i in range(len(a)):
i = str(i + 1)
print(«Введите элемент массива » + i, end = » «)
i = int(i)
i = i — 1
a = int(input())
print(«»)
for i in range(len(a)):
a = a * 2
for i in range(len(a)):
print(a, end = » «)Алгоритм поиска минимального значения массива в python
Нужно перебрать все элементы массива и каждый элемент сравнить с текущим минимумом. Если текущий элемент меньше текущего минимума, то этот элемент становится текущим минимумом.Алгоритм поиска максимального значения массива в python.
Аналогично, для поиска максимального значения нужно перебрать и сравнить каждый элемент с текущим максимумом. Если текущий элемент больше текущего максимума, то текущий максимум приравнивается к этому элементу.
Пример. Программа запрашивает значения элементов массива и выводит минимальное и максимальное значения на экран.a = * 9
for i in range(len(a) — 1):
i = str(i + 1)
print(«Введите элемент массива » + i, end = » «)
i = int(i)
a = int(input())
min = a
max = a
for i in range(len(a)):
if (a< min):
min = a
if (a > max):
max = a
min = str(min)
max = str(max)
print(«Минимальное значение = » + min)
print(«Максимальное значение = » + max)
Представление своих классов
Определяет поведение функции , вызванной для экземпляра вашего класса.
Определяет поведение функции , вызыванной для экземпляра вашего класса. Главное отличие от в целевой аудитории. больше предназначен для машинно-ориентированного вывода (более того, это часто должен быть валидный код на Питоне), а предназначен для чтения людьми.
Определяет поведение функции , вызыванной для экземпляра вашего класса. похож на , но возвращает строку в юникоде. Будте осторожны: если клиент вызывает на экземпляре вашего класса, а вы определили только , то это не будет работать. Постарайтесь всегда определять для случая, когда кто-то не имеет такой роскоши как юникод.
Определяет поведение, когда экземпляр вашего класса используется в форматировании строк нового стиля. Например, приведёт к вызову . Это может быть полезно для определения ваших собственных числовых или строковых типов, которым вы можете захотеть предоставить какие-нибудь специальные опции форматирования.
Определяет поведение функции , вызыванной для экземпляра вашего класса. Метод должен возвращать целочисленное значение, которое будет использоваться для быстрого сравнения ключей в словарях. Заметьте, что в таком случае обычно нужно определять и тоже. Руководствуйтесь следующим правилом: подразумевает .
Определяет поведение функции , вызванной для экземпляра вашего класса. Должна вернуть True или False, в зависимости от того, когда вы считаете экземпляр соответствующим True или False.
Определяет поведение функции , вызванной на экземпляре вашего класса. Этот метод должен возвращать пользователю список атрибутов
Обычно, определение не требуется, но может быть жизненно важно для интерактивного использования вашего класса, если вы переопределили или (с которыми вы встретитесь в следующей части), или каким-либо другим образом динамически создаёте атрибуты.
Определяет поведение функции , вызыванной на экземпляре вашего класса. Метод должен вернуть размер вашего объекта в байтах
Он главным образом полезен для классов, определённых в расширениях на C, но всё-равно полезно о нём знать.
Ввод списка (массива) в языке Питон
- Простой вариант ввода списка и его вывода:
L= L = int(input()) for i in range(5) # при вводе 1 2 3 4 5 print (L) # вывод: 1 2 3 4 5 |
Функция int здесь используется для того, чтобы строка, введенная пользователем, преобразовывалась в целые числа.
Как уже рассмотрено выше, список можно выводить целым и поэлементно:
# вывод целого списка (массива) print (L) # поэлементный вывод списка (массива) for i in range(5): print ( Li, end = " " ) |
Задание Python 4_7:
Необходимо задать список (массив) из шести элементов; заполнить его вводимыми значениями и вывести элементы на экран. Использовать два цикла: первый — для ввода элементов, второй — для вывода.
Замечание: Для вывода через «,» используйте следующий синтаксис:
print ( Li, end = ", " ) |
Пример результата:
введите элементы массива: 3.0 0.8 0.56 4.3 23.8 0.7 Массив = 3, 0.8, 0.56, 4.3, 23.8, 0.7
Задание Python 4_8:
Заполните список случайными числами в диапазоне 20..100 и подсчитайте отдельно число чётных и нечётных элементов. Использовать цикл.
Замечание: .
Задание Python 4_9: Найдите минимальный элемент списка. Выведите элемент и его индекс. Список из 10 элементов инициализируйте случайными числами. Для перебора элементов списка использовать цикл.
Пример результата:
9 5 4 22 23 7 3 16 16 8 Минимальный элемент списка L7=3 |
Решение системы линейных уравнений
http-equiv=»Content-Type» content=»text/html;charset=UTF-8″>kquote class=»wp-block-quote»>
В заключение мы рассмотрим последнюю из самых распространённых операций с матрицами – решение системы линейных уравнений.
Напомню, что система линейных уравнений имеет вид
где A – матрица, x – вектор-столбец искомых значений, b – вектор чисел. Решение, конечно же, состоит в умножении обоих частей уравнений на матрицу, обратную A:
Это корректная операция, поскольку предполагается, что A является квадратной матрицей, что значит, что она обратима. Тогда x имеет единственное решение. Другими словами, если размерность x равна D, то у нас есть D уравнений с D неизвестными.
Тут не должно возникнуть никаких сложностей, поскольку у нас уже есть весь инструментарий, необходимый для такого рода вычислений. Вы уже видели, как находится обратная матрица и как производить умножение матриц, а именно эти две вещи нам и нужны.
Решим пример. A у нас будет матрицей
Это корректная операция, поскольку предполагается, что A является квадратной матрицей, что значит, что она обратима. Тогда x имеет единственное решение. Другими словами, если размерность x равна D, то у нас есть D уравнений с D неизвестными.
Тут не должно возникнуть никаких сложностей, поскольку у нас уже есть весь инструментарий, необходимый для такого рода вычислений. Вы уже видели, как находится обратная матрица и как производить умножение матриц, а именно эти две вещи нам и нужны.
Решим пример. A у нас будет матрицей
b у нас будет вектором :
b = np.array()
Решением будет
x = np.linalg.inv(A).dot(b)
Итак, решением являются числа 0 и 0,5. Для проверки попробуйте решить этот пример вручную.
Конечно же, ввиду очень частого проведения такого рода вычислений, есть способ и получше – с помощью функции с соответствующим названием solve. Поэтому можно записать
x = np.linalg.solve(A, b)
И получим тот же ответ.
Если вы когда-либо прежде писали код в MATLAB, то могли заметить, что при попытке использовать метод inv MATLAB выдаёт предупреждение и сообщает, что есть и более эффективный способ вычислений. В MATLAB он называется не solve, но по сути это тот же самый алгоритм, и он действительно куда более эффективен и точен. Поэтому если у вас когда-нибудь возникнет необходимость решить подобного рода уравнение, никогда не пользуетесь inv. Всегда используйте solve.
Текстовая задача
Давайте разберём несложный пример, чтобы попрактиковаться в использовании функции solve.
Итак, поставим задачу. На небольшой ярмарке входная плата составляет 1,5 доллара для ребёнка и 4 доллара для взрослого. Однажды за день ярмарку посетило 2200 человек; при этом было собрано 5050 долларов входной платы. Сколько детей и сколько взрослых посетили ярмарку в этот день?
Итак, обозначим количество детей через X1, а количество взрослых – через X2. Мы знаем, что
Мы также знаем, что
Мы также знаем, что
Обратите внимание, что это линейное уравнение, где A равно:
а b равно :
а b равно :
Подставим эти значения в Numpy и найдём решение:
A = np.array(, ])
b = np.array()
np.linalg.solve(A, b)
Получаем ответ: 1500 детей и 700 взрослых. Попробуйте также решить это уравнение вручную, чтобы проверить ответ.
Интегральные функции
Есть и функции для решения интегралов. В их числе как обычные дифференциальные интеграторы, так и методы трапеций.
В SciPy представлена функция , которая занимается вычислением интеграла функции с одной переменной. Границы могут быть ±∞ (±) для обозначения бесконечных пределов. Синтаксис этой функции следующий:
А здесь она внедрена в пределах и (могут быть бесконечностями).
В этом примере функция находится в пределах 0 и 1. После выполнения вывод будет такой:
Двойные интегральные функции
SciPy включает также и , которая используется для вычисления двойных интегралов. Двойной интеграл, как известно, состоит из двух реальных переменных. Функция принимает функцию, которую нужно интегрировать, в качестве параметра, а также 4 переменных: две границы и функции и .
Пример:
Вывод:
В SciPy есть другие функции для вычисления тройных интегралов, n интегралов, интегралов Ромберга и других. О них можно узнать подробнее с помощью .
Функции оптимизации
В есть часто используемые алгоритмы оптимизации:
- Неограниченная и ограниченная минимизация многомерных скалярных функций, то есть (например, Алгоритм Бройдена — Флетчера — Гольдфарба — Шанно, метод сопряженных градиентов, метод Нелдера — Мида и так далее)
- Глобальная оптимизация (дифференциальная эволюция, двойной отжиг и т. д.)
- Минимизация наименьших квадратов и подбор кривой (метод наименьших квадратов, приближение с помощью кривых и т. д.)
- Минимизаторы скалярных одномерных функций и численное решение уравнений (минимизация скаляра и скаляр корня)
- Решатели систем многомерных уравнений с помощью таких алгоритмов, как Пауэлла, Левендберга — Марквардта.
Функция Розенброка
Функция Розенброка () — это тестовая проблема для оптимизационных алгоритмов, основанных на градиентах. В SciPy она определена следующим образом:
Пример:
Вывод:
Nelder-Mead
Это числовой метод, который часто используется для поиска минимума/максимума функции в многомерном пространстве. В следующем примере метод использован вместе с алгоритмом Нелдера — Мида.
Пример:
Вывод:
7.3. Статистика
Над данными в массивах можно производить определенные вычисления, однако, не менее часто требуется эти данные как-то анализировать. Зачастую, в этом случае мы обращаемся к статистике, некоторые функции которой тоже имеются в NumPy. Данные функции могут применять как ко всем элементам массива, так и к элементам, расположенным вдоль определенной оси.
Элементарные статистические функции:
Средние значения элементов массива и их отклонения:
Корреляционные коэфициенты и ковариационные матрицы величин:
Так же NumPy предоставляет функции для вычисления гистограмм наборов данных различной размерности и некоторые другие статистичские функции.
Обработка текста в NumPy на примерах
Когда дело доходит до текста, подход несколько меняется. Цифровое представление текста предполагает создание некого , то есть инвентаря всех уникальных слов, которые бы распознавались моделью, а также векторно (embedding step). Попробуем представить в цифровой форме цитату из стихотворения арабского поэта Антара ибн Шаддада, переведенную на английский язык:
“Have the bards who preceded me left any theme unsung?”
Перед переводом данного предложения в нужную цифровую форму модель должна будет проанализировать огромное количество текста. Здесь можно обработать небольшой набор данный, после чего использовать его для создания словаря из 71 290 слов.
Предложение может быть разбито на массив токенов, что будут словами или частями слов в зависимости от установленных общих правил:
Затем в данной таблице словаря вместо каждого слова мы ставим его :
Однако данные все еще не обладают достаточным количеством информации о модели как таковой. Поэтому перед передачей последовательности слов в модель токены/слова должны быть заменены их векторными представлениями. В данном случае используется 50-мерное векторное представление Word2vec.
Здесь ясно видно, что у массива NumPy есть несколько размерностей . На практике все выглядит несколько иначе, однако данное визуальное представление более понятно для разъяснения общих принципов работы.
Для лучшей производительности модели глубокого обучения обычно сохраняют первую размерность для пакета. Это происходит из-за того, что тренировка модели происходит быстрее, если несколько примеров проходят тренировку параллельно. Здесь особенно полезным будет . Например, такая модель, как BERT, будет ожидать ввода в форме: .
Теперь мы получили числовой том, с которым модель может работать и делать полезные вещи. Некоторые строки остались пустыми, однако они могут быть заполнены другими примерами, на которых модель может тренироваться или делать прогнозы.
(На заметку: Поэма, строчку из которой мы использовали в примере, увековечила своего автора в веках. Будучи незаконнорожденным сыном главы племени от рабыни, Антара ибн Шаддан мастерски владел языком поэзии. Вокруг исторической фигуры поэта сложились мифы и легенды, а его стихи стали частью классической арабской литературы).
Копирование
-
Определяет поведение для экземпляра вашего класса. возвращает поверхностную копию вашего объекта — это означает, что хоть сам объект и создан заново, все его данные ссылаются на данные оригинального объекта. И при изменении данных нового объекта, изменения будут происходить и в оригинальном.
-
Определяет поведение для экземпляров вашего класса. возвращает глубокую копию вашего объекта — копируются и объект и его данные. это кэш предыдущих скопированных объектов, он предназначен для оптимизации копирования и предотвращения бесконечной рекурсии, когда копируются рекурсивные структуры данных. Когда вы хотите полностью скопировать какой-нибудь конкретный атрибут, вызовите на нём с первым параметром .
Tricks and Tips¶
Here we give a list of short and useful tips.
“Automatic” Reshaping
To change the dimensions of an array, you can omit one of the sizes
which will then be deduced automatically:
>>> a = np.arange(30)
>>> b = a.reshape((2, -1, 3)) # -1 means "whatever is needed"
>>> b.shape
(2, 5, 3)
>>> b
array(,
,
,
,
],
,
,
,
,
]])
Vector Stacking
How do we construct a 2D array from a list of equally-sized row vectors?
In MATLAB this is quite easy: if and are two vectors of the
same length you only need do . In NumPy this works via the
functions , , and ,
depending on the dimension in which the stacking is to be done. For
example:
>>> x = np.arange(,10,2)
>>> y = np.arange(5)
>>> m = np.vstack()
>>> m
array(,
])
>>> xy = np.hstack()
>>> xy
array()
The logic behind those functions in more than two dimensions can be
strange.
See also
Runtastic
Функции (методы) для расчета статистик в Numpy
Ниже, в таблице, приведены методы объекта ndarray (или matrix), которые, как мы помним из раздела выше, могут быть также вызваны как функции библиотеки Numpy, для расчета статистик по данным массива.
| Имя метода | Описание |
| argmax | Индексы элементов с максимальным значением (по осям) |
| argmin | Индексы элементов с минимальным значением (по осям) |
| max | Максимальные значения элементов (по осям) |
| min | Минимальные значения элементов (по осям) |
| mean | Средние значения элементов (по осям) |
| prod | Произведение всех элементов (по осям) |
| std | Стандартное отклонение (по осям) |
| sum | Сумма всех элементов (по осям) |
| var | Дисперсия (по осям) |
Вычислим некоторые из представленных выше статистик.
>>> m.mean()
4.833333333333333
>>> m.mean(axis=1)
matrix(,
,
])
>>> m.sum()
58
>>> m.sum(axis=0)
matrix(])
Примеры работы с NumPy
Подытожим все вышесказанное. Вот несколько примеров полезных инструментов NumPy, которые могут значительно облегчить процесс написания кода.
Математические формулы NumPy
Необходимость внедрения математических формул, которые будут работать с матрицами и векторами, является главной причиной использования NumPy. Именно поэтому NumPy пользуется большой популярностью среди представителей науки. В качестве примера рассмотрим формулу , которая является центральной для контролируемых моделей машинного обучения, что решают проблемы регрессии:
Реализовать данную формулу в NumPy довольно легко:
Главное достоинство NumPy в том, что его не заботит, если и содержат одно или тысячи значение (до тех пор, пока они оба одного размера). Рассмотрим пример, последовательно изучив четыре операции в следующей строке кода:
У обоих векторов и по три значения. Это значит, что в данном случае равно трем. После выполнения указанного выше вычитания мы получим значения, которые будут выглядеть следующим образом:
Затем мы можем возвести значения вектора в квадрат:
Теперь мы вычисляем эти значения:
Таким образом мы получаем значение ошибки некого прогноза и за качество модели.
Представление данных NumPy
Задумайтесь о всех тех типах данных, которыми вам понадобится оперировать, создавая различные модели работы (электронные таблицы, изображения, аудио и так далее). Очень многие типы могут быть представлены как n-мерные массивы:
7.4. Генерация случайных значений
Очень многие вычислительные методы требуют генерации случайных значений. В некоторых ситуациях, на генерируемые данные накладываются очень строгие и высокие требования. NumPy содержит функции для генерации простых случайных данных, функции генерации случайных перестановок, а так же большое количество функций для гернерации случайных чисел с всевозможными вероятностными распределениями.
Получение простых случайных данных:
Перестановки:
NumPy предоставляет порядка 30 функций, позволяющих генерировать случайные числа с самыми разными вероятностными распределениями:
Вы так же имеете доступ к состоянию генератора случайных чисел, а так же можете управлять им: