Корреляционный анализ
Содержание:
- Hard Reset средствами самой системы Android
- Множественная корреляция, её коэффициент
- Открытие загрузочной флешки через BIOS
- Предвзятость средств массовой информации
- Линейный коэффициент корреляции Пирсона
- Оставить комментарий
- Корреляционный анализ
- Список литературы
- Корреляционные матрицы
- Критерии и методы
- КРИТЕРИЙ СПИРМЕНА
- Интересные профессии
Hard Reset средствами самой системы Android
Множественная корреляция, её коэффициент
Множественная корреляция — это вероятностная зависимость между одной величиной с
одной стороны, и одновременно несколькими другими ,
с другой стороны.
То есть, в отличие от парной корреляции, при которой
на изменения зависимой (результирующей) переменной влияет одна независимая (объясняющая) переменная,
при множественной корреляции независимых (объясняющих) переменных две или больше.
Цель корреляционного анализа в случае множественной корреляции — установить, есть ли зависимость между
переменными и насколько тесно связаны между собой зависимая переменная, с одной стороны, и независимые
переменные, с другой стороны, и зависят ли друг от друга независимые переменные .
Для того чтобы можно было бы применять модель множественной линейной регрессии, прежде, при анализе
множественной корреляции должны быть установлены следующие факты:
- зависимая переменная тесно зависит от независимых переменных (тесноту связи, как и в случае
парной корреляции, показывают ); - нет тесной зависимости между независимыми переменными.
Коэффициент множественной корреляции в случае двухфакторной корреляции рассчитывается по следующей формуле:
.
Коэффициенты множественной корреляции между зависимой переменной
и независимыми переменными
записываются в корреляционную матрицу:
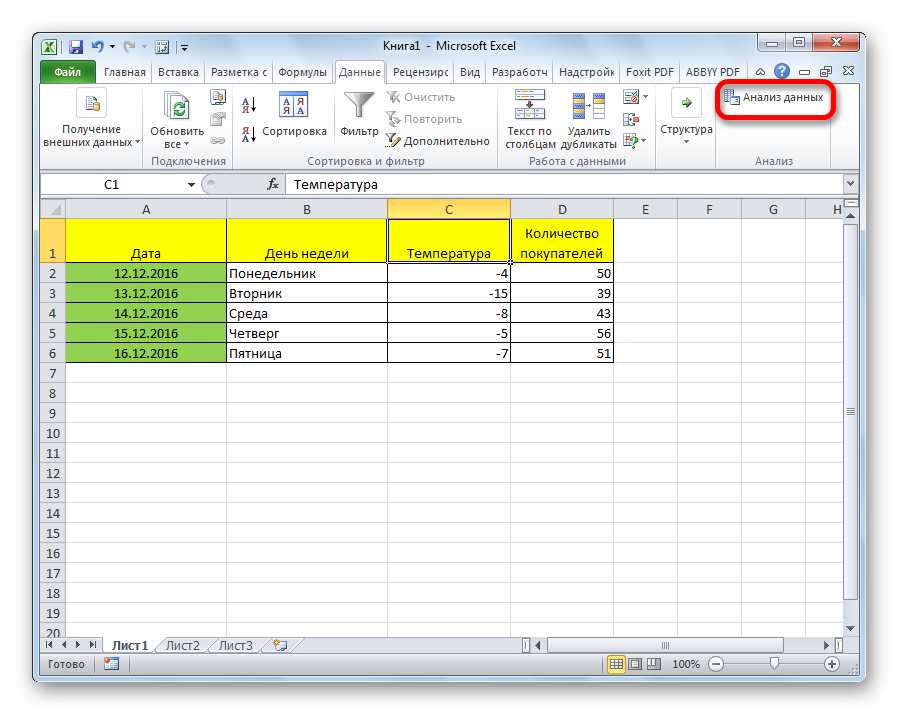
Пример 1. Аналитик предприятия решил проверить факторы, которые
влияют на размер заработной платы сотрудников . Предварительно
в качестве объясняющих факторов выбраны: возраст сотрудника ,
стаж работы , оценка теста для приёма
на работу и число подчинённых
сотрудников . Случайно были выбраны
200 сотрудников, данные которых были обобщены. В результате была получена следующая корреляционная матрица:
| 1 | |||||
| -0,27 | 1 | ||||
| 0,78 | -0,63 | 1 | |||
| -0,83 | 0,47 | -0,89 | 1 | ||
| 0,65 | -0,46 | 0,17 | -0,21 | 1 |
Установить, какие переменные можно выбрать как независимые, для того, чтобы далее
можно было бы строить модель множественной регрессии.
Решение.
Корреляционная матрица показывает, что между переменными:
- и — слабая линейная связь: -0,27;
- и — средне тесная положительная линейная связь: 0,78;
- и — тесная отрицательная линейная связь: -0,83;
- и — средне тесная линейная связь: 0,65;
- и — тесная отрицательная линейная связь: -0,89;
- и — слабая линейная связь: 0,17;
- и — слабая линейная связь: -0,21.
Таким образом, не следует включать в число переменных, влияющих на размер заработной
платы возраст сотрудников . Так как
между независимыми переменными и
установлена тесная отрицательная связь,
не включаем в число переменных, влияющих на размер заработной платы стаж работы .
Выбираем в качестве независимых переменных оценку теста для приёма
на работу и число подчинённых
сотрудников .
Чтобы установить тесноту связи между заработной платой сотрудников ,
с одной стороны, и оценкой теста для приёма
на работу и числом подчинённых
сотрудников , с другой стороны,
вычислим коэффициент множественной (двухфакторной) корреляции:
Таким образом, между заработной платой сотрудников, с одной стороны, и
оценкой теста для приёма на работу и числом подчинённых, с другой стороны, существует тесная линейная
связь.
Как показывает пример выше, в исследованиях поведения человека,
как и во многих других направлениях, важно установить, какие факторы из многих действительно влияют на
результат при учете влияния всех остальных факторов
Открытие загрузочной флешки через BIOS
Мало только сделать загрузочный флеш-накопитель. Случается так, что система перестаёт работать. В таком случае образ, записанный на флешку, необходимо открыть через настройки BIOS. Независимо от времени выпуска BIOS, названия, находящиеся в нем, остаются практически неизменными.
После того как вы зашли в BIOS, необходимо открыть «Advanced BIOS Features», в которой размещены устройства, в порядке запуска. Например, сначала загружается жесткий диск, при его отказе система обращается к CDROM. Не найдя системы и на нем, она переходит к USB-HDD. Что нам и надо. Поставив на первое место USB-HDD, сохраняем настройки и выходим из BIOS. При перезагрузке появится меню установки ОС. На некоторых современных системных платах существует специальное Boot Menu, войти в которое можно при загрузке ПК, нажимая F8 или F12, в зависимости от фирмы-изготовителя «материнки», где очень просто можно выбрать загрузку ПК с записанного USB-накопителя. При загрузке ОС через BIOS может возникнуть несколько проблем, таких как:
- Системная плата не может поддерживать загрузку с внешнего устройства. Это возможно при таком случае, когда «материнка» была сделана до 2003 года;
- Обнаружение некорректной загрузочной флеш-карты. Вероятно, при записи операционной системы были допущены какие-либо ошибки. Проверьте загрузочную флешку на другом ПК;
- Отключение контроллера USB в BIOS.
Предвзятость средств массовой информации
Рассмотрим, как наличие корреляционной связи может быть неправильно истолковано. Группу британских студентов, отличающихся плохим поведением, опросили относительно того, курят ли их родители. Потом тест опубликовали в газете. Результат показал сильную корреляцию между курением родителей и правонарушениями их детей. Профессор, который проводил это исследование, даже предложил поместить на пачки сигарет предупреждение об этом. Однако существует целый ряд проблем с таким выводом. Во-первых, корреляция не показывает, какая из величин является независимой. Поэтому вполне можно предположить, что пагубная привычка родителей вызвана непослушанием детей. Во-вторых, нельзя с уверенностью сказать, что обе проблемы не появились из-за какого-то третьего фактора. Например, низкого дохода семей. Следует отметить эмоциональный аспект первоначальных выводов профессора, который проводил исследование. Он был ярым противником курения. Поэтому нет ничего удивительного в том, что он интерпретировал результаты своего исследования именно так.
Линейный коэффициент корреляции Пирсона
Обнаружение взаимосвязей между явлениями – одна из главных задач статистического анализа. На то есть две причины. Первая. Если известно, что один процесс зависит от другого, то на первый можно оказывать влияние через второй. Вторая. Даже если причинно-следственная связь отсутствует, то по изменению одного показателя можно предсказать изменение другого.
Взаимосвязь двух переменных проявляется в совместной вариации: при изменении одного показателя имеет место тенденция изменения другого. Такая взаимосвязь называется корреляцией, а раздел статистики, который занимается взаимосвязями – корреляционный анализ.
Корреляция – это, простыми словами, взаимосвязанное изменение показателей. Она характеризуется направлением, формой и теснотой. Ниже представлены примеры корреляционной связи.
При положительном отклонении X от своей средней, Y также в большинстве случаев отклоняется в положительную сторону от своей средней. Для X меньше среднего, Y, как правило, тоже ниже среднего.
Это прямая или положительная корреляция.
Бывает обратная или отрицательная корреляция, когда положительное отклонение от средней X ассоциируется с отрицательным отклонением от средней Y или наоборот.
Линейность корреляции проявляется в том, что точки расположены вдоль прямой линии. Положительный или отрицательный наклон такой линии определяется направлением взаимосвязи.
Крайне важная характеристика корреляции – теснота. Чем теснее взаимосвязь, тем ближе к прямой точки на диаграмме. Как же ее измерить?
Складывать отклонения каждого показателя от своей средней нет смысла, получим нуль. Похожая проблема встречалась при измерении вариации, а точнее дисперсии. Там эту проблему обходят через возведение каждого отклонения в квадрат.
Квадрат отклонения от средней измеряет вариацию показателя как бы относительно самого себя. Если второй множитель в числителе заменить на отклонение от средней второго показателя, то получится совместная вариация двух переменных, которая называется ковариацией.
Чем больше пар имеют одинаковый знак отклонения от средней, тем больше сумма в числителе (произведение двух отрицательных чисел также дает положительное число).
Оставить комментарий
Корреляционный анализ
Корреляционный анализ — метод обработки статистических данных, с помощью которого измеряется теснота связи между двумя или более переменными. Корреляционный анализ тесно связан с регрессионным анализом (также часто встречается термин «корреляционно-регрессионный анализ», который является более общим статистическим понятием), с его помощью определяют необходимость включения тех или иных факторов в уравнение множественной регрессии, а также оценивают полученное уравнение регрессии на соответствие выявленным связям (используя коэффициент детерминации).
Ограничения корреляционного анализа
Множество корреляционных полей. Распределения значений (x,y){\displaystyle (x,y)} с соответствующими коэффициентами корреляций для каждого из них. Коэффициент корреляции отражает «зашумлённость» линейной зависимости (верхняя строка), но не описывает наклон линейной зависимости (средняя строка), и совсем не подходит для описания сложных, нелинейных зависимостей (нижняя строка). Для распределения, показанного в центре рисунка, коэффициент корреляции не определен, так как дисперсия y равна нулю.
- Применение возможно при наличии достаточного количества наблюдений для изучения. На практике считается, что число наблюдений должно не менее чем в 5-6 раз превышать число факторов (также встречается рекомендация использовать пропорцию, не менее чем в 10 раз превышающую количество факторов). В случае если число наблюдений превышает количество факторов в десятки раз, в действие вступает закон больших чисел, который обеспечивает взаимопогашение случайных колебаний.
- Необходимо, чтобы совокупность значений всех факторных и результативного признаков подчинялась многомерному нормальному распределению. В случае если объём совокупности недостаточен для проведения формального тестирования на нормальность распределения, то закон распределения определяется визуально на основе корреляционного поля. Если в расположении точек на этом поле наблюдается линейная тенденция, то можно предположить, что совокупность исходных данных подчиняется нормальному закону распределения..
- Исходная совокупность значений должна быть качественно однородной.
- Сам по себе факт корреляционной зависимости не даёт основания утверждать, что одна из переменных предшествует или является причиной изменений, или то, что переменные вообще причинно связаны между собой, а не наблюдается действие третьего фактора.
Область применения
Данный метод обработки статистических данных весьма популярен в экономике, астрофизике и социальных науках (в частности в психологии и социологии), хотя сфера применения коэффициентов корреляции обширна: контроль качества промышленной продукции, металловедение, агрохимия, гидробиология, биометрия и прочие. В различных прикладных отраслях приняты разные границы интервалов для оценки тесноты и значимости связи.
Популярность метода обусловлена двумя моментами: коэффициенты корреляции относительно просты в подсчете, их применение не требует специальной математической подготовки. В сочетании с простотой интерпретации, простота применения коэффициента привела к его широкому распространению в сфере анализа статистических данных.
Список литературы
- Аблеева, А. М. Формирование фонда оценочных средств в условиях ФГОС / А. М. Аблеева, Г. А. Салимова // Актуальные проблемы преподавания социально-гуманитарных, естественно — научных и технических дисциплин в условиях модернизации высшей школы : материалы международной научно-методической конференции, 4-5 апреля 2014 г. / Башкирский ГАУ, Факультет информационных технологий и управления. — Уфа, 2014. — С. 11-14.
- Ганиева, А.М. Статистический анализ занятости и безработицы / А.М. Ганиева, Т.Н. Лубова // Актуальные вопросы экономико-статистического исследования и информационных технологий: сб. науч. ст.: посвящается к 40-летию создания кафедры «Статистики и информационных систем в экономике» / Башкирский ГАУ. — Уфа, 2011. — С. 315-316.
- Исмагилов, Р. Р. Творческая группа — эффективная форма организации научных исследований в высшей школе / Р. Р. Исмагилов, М. Х. Уразлин, Д. Р. Исламгулов // Научно-технический и научно-образовательный комплексы региона : проблемы и перспективы развития : материалы научно-практической конференции / Академия наук РБ, УГАТУ. — Уфа, 1999. — С. 105-106.
- Исламгулов, Д.Р. Компетентностный подход в обучении: оценка качества образования / Д.Р. Исламгулов, Т.Н. Лубова, И.Р. Исламгулова // Современный научный вестник. – 2015. – Т. 7. — № 1. – С. 62-69.
- Исламгулов, Д. Р. Научно-исследовательская работа студентов — важнейший элемент подготовки специалистов в аграрном вузе / Д. Р. Исламгулов // Проблемы практической подготовки студентов в вузе на современном этапе и пути их решения : сб. материалов науч.-метод. конф., 24 апреля 2007 года / Башкирский ГАУ. — Уфа, 2007. — С. 20-22.
- Лубова, Т.Н. Основа реализации федерального государственного образовательного стандарта – компетентностный подход / Т.Н. Лубова, Д.Р. Исламгулов, И.Р. Исламгулова// БЪДЕЩИТЕ ИЗСЛЕДОВАНИЯ – 2016: Материали за XII Международна научна практична конференция, 15-22 февруари 2016. – София: Бял ГРАД-БГ ООД, 2016. – Том 4 Педагогически науки. – C. 80-85.
- Лубова, Т.Н. Новые образовательные стандарты: особенности реализации / Т.Н. Лубова, Д.Р. Исламгулов // Современный научный вестник. – 2015. – Т. 7. — № 1. – С. 79-84.
- Лубова, Т.Н. Организация самостоятельной работы обучающихся / Т.Н. Лубова, Д.Р. Исламгулов // Реализация образовательных программ высшего образования в рамках ФГОС ВО: материалы Всероссийской научно-методической конференции в рамках выездного совещания НМС по природообустройству и водопользованию Федерального УМО в системе ВО. / Башкирский ГАУ. — Уфа, 2016. — С. 214-219.
- Лубова, Т.Н. Основа реализации федерального государственного образовательного стандарта – компетентностный подход / Т.Н. Лубова, Д.Р. Исламгулов, И.Р. Исламгулова // Современный научный вестник. – 2015. – Т. 7. — № 1. – С. 85-93.
- Саубанова, Л.М. Уровень демографической нагрузки / Л.М. Саубанова, Т.Н. Лубова // Актуальные вопросы экономико-статистического исследования и информационных технологий: сб. науч. ст.: посвящается к 40-летию создания кафедры «Статистики и информационных систем в экономике» / Башкирский ГАУ. — Уфа, 2011. — С. 321-322.
- Фахруллина, А.Р. Статистический анализ инфляции в России / А.Р. Фахруллина, Т.Н. Лубова // Актуальные вопросы экономико-статистического исследования и информационных технологий: сб. науч. ст.: посвящается к 40-летию создания кафедры «Статистики и информационных систем в экономике» / Башкирский ГАУ. — Уфа, 2011. — С. 323-324.
- Фархутдинова, А.Т. Рынок труда в Республике Башкортостан в 2012 году / А.Т. Фархутдинова, Т.Н. Лубова // Студенческий научный форум. Материалы V Международной студенческой электронной научной конференции: электронная научная конференция (электронный сборник). Российская академия естествознания. 2013.
Корреляционные матрицы
Корреляционная матрица случайных величин — это матрица, элементом которой является . Если меры корреляции используется коэффициенты продукта момент, корреляционная матрица является таким же , как ковариационная матрица из стандартизованных случайных величин для . Это применимо как к матрице корреляций совокупности (в этом случае — стандартное отклонение совокупности), так и к матрице корреляций выборки (в этом случае означает стандартное отклонение выборки). Следовательно, каждая матрица обязательно является положительно-полуопределенной . Более того, корреляционная матрица является строго положительно определенной, если никакая переменная не может иметь все свои значения, точно сгенерированные как линейная функция значений других.
п{\ displaystyle n}Икс1,…,Иксп{\ Displaystyle X_ {1}, \ ldots, X_ {n}}п×п{\ Displaystyle п \ раз п}(я,j){\ displaystyle (я, j)}корр(Икся,Иксj){\ displaystyle \ operatorname {corr} (X_ {i}, X_ {j})} Иксяσ(Икся){\ Displaystyle X_ {i} / \ sigma (X_ {i})}язнак равно1,…,п{\ Displaystyle я = 1, \ точки, п}σ{\ displaystyle \ sigma}σ{\ displaystyle \ sigma}
Матрица корреляции является симметричной, поскольку корреляция между и такая же, как корреляция между и .
Икся{\ displaystyle X_ {i}}Иксj{\ displaystyle X_ {j}}Иксj{\ displaystyle X_ {j}}Икся{\ displaystyle X_ {i}}
Матрица корреляции появляется, например, в одной формуле для , меры согласия в множественной регрессии .
В статистическом моделировании матрицы корреляции, представляющие взаимосвязи между переменными, подразделяются на различные структуры корреляции, которые различаются такими факторами, как количество параметров, необходимых для их оценки. Например, в заменяемой корреляционной матрице все пары переменных моделируются как имеющие одинаковую корреляцию, поэтому все недиагональные элементы матрицы равны друг другу. С другой стороны, авторегрессионная матрица часто используется, когда переменные представляют собой временной ряд, поскольку корреляции, вероятно, будут больше, когда измерения ближе по времени. Другие примеры включают независимый, неструктурированный, M-зависимый и Toeplitz.
Критерии и методы
КРИТЕРИЙ СПИРМЕНА
Коэффициент ранговой корреляции Спирмена – это непараметрический метод, который используется с целью статистического изучения связи между явлениями. В этом случае определяется фактическая степень параллелизма между двумя количественными рядами изучаемых признаков и дается оценка тесноты установленной связи с помощью количественно выраженного коэффициента.
Чарльз Эдвард Спирмен
1. История разработки коэффициента ранговой корреляции
Данный критерий был разработан и предложен для проведения корреляционного анализа в 1904 году Чарльзом Эдвардом Спирменом, английским психологом, профессором Лондонского и Честерфилдского университетов.
2. Для чего используется коэффициент Спирмена?
Коэффициент ранговой корреляции Спирмена используется для выявления и оценки тесноты связи между двумя рядами сопоставляемых количественных показателей. В том случае, если ранги показателей, упорядоченных по степени возрастания или убывания, в большинстве случаев совпадают (большему значению одного показателя соответствует большее значение другого показателя — например, при сопоставлении роста пациента и его массы тела), делается вывод о наличии прямой корреляционной связи. Если ранги показателей имеют противоположную направленность (большему значению одного показателя соответствует меньшее значение другого — например, при сопоставлении возраста и частоты сердечных сокращений), то говорят об обратной связи между показателями.
- Коэффициент корреляции Спирмена обладает следующими свойствами:
- Коэффициент корреляции может принимать значения от минус единицы до единицы, причем при rs=1 имеет место строго прямая связь, а при rs= -1 – строго обратная связь.
- Если коэффициент корреляции отрицательный, то имеет место обратная связь, если положительный, то – прямая связь.
- Если коэффициент корреляции равен нулю, то связь между величинами практически отсутствует.
- Чем ближе модуль коэффициента корреляции к единице, тем более сильной является связь между измеряемыми величинами.
3. В каких случаях можно использовать коэффициент Спирмена?
В связи с тем, что коэффициент является методом непараметрического анализа, проверка на нормальность распределения не требуется.
Сопоставляемые показатели могут быть измерены как в непрерывной шкале (например, число эритроцитов в 1 мкл крови), так и в порядковой (например, баллы экспертной оценки от 1 до 5).
Эффективность и качество оценки методом Спирмена снижается, если разница между различными значениями какой-либо из измеряемых величин достаточно велика. Не рекомендуется использовать коэффициент Спирмена, если имеет место неравномерное распределение значений измеряемой величины.
4. Как рассчитать коэффициент Спирмена?
Расчет коэффициента ранговой корреляции Спирмена включает следующие этапы:
- Сопоставить каждому из признаков их порядковый номер (ранг) по возрастанию или убыванию.
- Определить разности рангов каждой пары сопоставляемых значений (d).
- Возвести в квадрат каждую разность и суммировать полученные результаты.
- Вычислить коэффициент корреляции рангов по формуле:
Определить статистическую значимость коэффициента при помощи t-критерия, рассчитанного по следующей формуле:
5. Как интерпретировать значение коэффициента Спирмена?
При использовании коэффициента ранговой корреляции условно оценивают тесноту связи между признаками, считая значения коэффициента меньше 0,3 — признаком слабой тесноты связи; значения более 0,3, но менее 0,7 — признаком умеренной тесноты связи, а значения 0,7 и более — признаком высокой тесноты связи.
Также для оценки тесноты связи может использоваться шкала Чеддока:
xy
Теснота (сила) корреляционной связи
менее 0.3
слабая
от 0.3 до 0.5
умеренная
от 0.5 до 0.7
заметная
от 0.7 до 0.9
высокая
более 0.9
весьма высокая
Статистическая значимость полученного коэффициента оценивается при помощи t-критерия Стьюдента. Если расчитанное значение t-критерия меньше табличного при заданном числе степеней свободы, статистическая значимость наблюдаемой взаимосвязи — отсутствует. Если больше, то корреляционная связь считается статистически значимой.
Интересные профессии
Стюардесса
Это одна из самых интересных профессий. Но стать стюардессой очень непросто
Очень важно иметь идеальную внешность и свободно владеть несколькими иностранными языками
Помимо этого, нужно все-таки получить специальное образование и пройти жесткий отбор. Но если вам это удастся, то интересная и насыщенная жизнь вам обеспечены. Правда задумайтесь о том, не станет ли данная профессия преградой на пути к семейному счастью, ведь постоянные разъезды редко нравятся мужьям.
Проводница
Это не такая романтическая профессия, как предыдущая, тем не менее, освоив ее, вы точно не будете скучать.
Стать проводницей намного проще, чем стюардессой. Здесь кастинги никто не устраивает и языки учить не заставляют. Тем не менее, закончит специализированное учебное заведение все же нужно.
Фотограф
Фотографы способны запечатлеть самые светлые моменты жизни любого человека. Частичка радости всегда передается от клиента к фотографу.
Казалось бы, что нет ничего проще, чем купит камеру и начать фотографировать. Но фотоискусству, как и любому другому ремеслу нужно учиться. Для того чтобы сделать карьеру успешного фотографа вы должны:
- Иметь хорошую технику и аксессуары;
- Пройти обучение;
- Много практиковаться.
Дизайнер
Дизайнер – не только интересная, но и творческая профессия. Если вы обладаете чувством вкуса, умеете красиво рисовать, ваша голова полна идей, а фантазия не имеет границ, то обязательно попробуйте свои силы в качестве дизайнера.
Конечно, стать профессионалом без получения должного образования у вас не получится. Только в учебных заведениях помогут раскрыть ваш талант и дадут все необходимые знания.
Менеджер по туризму
Любое туристическое агентство в своем штате имеет одного или нескольких менеджеров по туризму.
Именно эти люди находят клиентов и продают им туры. Чаще всего такие специалисты сами посетили все туры, сопровождая туристов. Они должны хорошо разбираться в специфике своей профессии и психологии людей. А этому их учат в колледжах и институтах.
Тренер вебинаров
Это очень молодая профессия, которая появилась после того, как интернет стал доступен всем и каждому.
Но для того чтобы такая деятельность приносила желаемый доход, вы должны обладать полезными знаниями, за передачу которых люди будут платить вам деньги.
Не думайте, что если вы расскажете как печь бисквит, вам кто-то заплатит хоть копейку.
Большим спросом пользуются вебинары, где тренер рассказывает, как зарабатывать деньги или учит методам влияния на людей, психологии, а также вебинары по материнству и грудному вскармливанию и т. д.
Также прочитайте:
- Работа в интернете на дому без вложений и без обмана
- Как заработать деньги в интернете — проверенные и актуальные способы
Флорист
Во все времена сердца женщин мужчины завоевывали при помощи шикарных букетов. А ведь такую красоту создают простые девушки и женщины. Если вы любите растения, а фантазия ваша безгранична, мы предлагаем стать флористом.
Для того чтобы освоить эту специальность, нужно иметь минимальные знания о растениях и чувство стиля. Если вы будете составлять хорошие композиции и обзаведетесь постоянными клиентами, то в будущем можно будет задуматься об открытие собственного дела.
Специалист по этикету
Во всех учебных заведениях ΧΧΙ века минимум времени уделяется вопросам этикета. А ведь умение держать себя в обществе это качество, которым должен владеть каждый человек. Но сейчас очень мало специалистов, которые могут обучить искусству этикета.
Из-за большого количества клиентов и небольшого количества преподавателей, специалисты по этикету без дела никогда не сидят.
Спортивный инструктор
Здоровый образ жизни на пике популярности. ПП и восстановление после родов — это вообще одни из ТОПовых направлений сегодня.
Многие люди поняли насколько важно вести активный образ жизни и массово начинают записываться в спортзалы. Попав туда, люди с большой охотой оплачивают услуги спортивных инструкторов, которые сопровождают их на протяжении всего занятия
Чаще всего в инструктора идут профессиональные спортсмены, которые по каким-то причинам решили оставить большой спорт.
Модельер
Вы в детстве шили наряды для кукол, а сейчас создаете одежду для себя? Тогда вам определенно нужно освоить профессию модельера.
Для того чтобы стать модельером, нужно уметь не только красиво рисовать, но и досконально знать швейное искусство. Чаще всего модельеры делают свою карьеру после того, как освоят профессию швеи, а потом несколько лет проработают в ателье.
Хореограф
Танцевать любят не только дети, но и взрослые. Именно поэтому все больше людей в сознательном возрасте записываются на уроки танцев.
Из-за того, что танцевальных направлений очень много, хореографы всегда найдут себе работу. Правда осваивают такую профессию девушки, которые танцами занимались или занимаются профессионально.
Вначале своей карьеры можно только преподавать уроки танцев, а через несколько лет скопить капитал и открыть свою хореографическую студию.