Задачи на проценты: считаем проценты с помощью пропорции

Что такое проценты?

Это слово произошло от английского словосочетания Pro Centum

Прочитав это словосочетание, вы наверняка обратили внимание, что там присутствует слово цент. От этого и происходит смысл процентов

Как известно, цент — одна сотая часть от доллара. Поэтому 1% — это и есть одна сотая часть от числа.

Сейчас в процентах измеряются многие финансовые показатели:

1. налоги;
2. доли в бизнесе;
3. доходность от инвестиций;
4. премии и штрафы;
5. инфляция.

И не только финансовые:

1. рождаемость и смертность;
2. статистика удачных и неудачных браков;
3. коэффициент полезного действия.

Пример 1. Водитель таксомоторной службы отработал смену. За день его выручка составила 5 тыс. рублей. Ему необходимо отдать службе такси комиссию с этих заказов — 15%. Чтобы узнать сумму, которую должен заплатить водитель, необходимо 5 тыс. умножить на 15, после чего разделить на 100. Мы получаем результат, равный 750 рублей. Как вы уже догадались, 15% — это 15 частей из ста.

Теперь мы приведём вам обратный пример с тем же водителем такси. Так, за смену он заработал 5 тыс. рублей. Он потратил определённую часть этих денег на обязательные расходы:

1. комиссию службе такси — 750 рублей;
2. мойку автомобиля — 250 рублей;
3. топливо — 1 тыс. рублей.

Итого у водителя остаётся 3 тыс. рублей. Из заработанных 5 тыс. рублей себе он забирает только 3. Теперь наша задача посчитать, какую часть от общей выручки он может смело положить к себе в карман. Для этого нам нужно разделить 3 тыс. на 5 тыс. После чего полученный результат, равный 0,6, умножить на 100%. Получается, водитель забирает себе в карман 60% от общей выручки.

Это интересно: разрядные слагаемые — что это?

Пример 2. Четыре акционера открыли бизнес. Спустя год упорной работы он начал приносить доходы. Партнёры решили делить прибыль поровну, то есть каждому достанется по 25% от прибыли. Нам нужно посчитать, сколько денег получит каждый из них.

Допустим, бизнес приносит доход 200 тысяч рублей в месяц. Чтобы посчитать прибыль каждого из акционеров, необходимо умножить 200 тыс. на 25, и разделить на 100. Получаем результат — 50 тыс. рублей.

Пример 3. Конверсия продаж. Менеджер по продажам предлагает услуги своей компании по телефону. За месяц он совершил 800 звонков. Заинтересовались в услугах компании 280 клиентов. Для подсчёта конверсии продаж необходимо 280 разделить на 800, после чего умножить на 100. Результат будет равен 35%.

Таблица основных показателей процентных величин

Если вы готовитесь к числовым тестам на проценты или доли, мы настоятельно рекомендуем потратить несколько часов и выучить данную таблицу. Это поможет сэкономить вам драгоценное время по время прохождения реального тестирования.

Доля	Десятичный	Процент
1/2	0,5	50%
1/3	0,333	33,333%
2/3	0,666	66,666%
1/4	0,25	25%
3/4	0,75	75%
1/5	0.2	20%
2/5	0,4	40%
3/5	0.6	60%
4/5	0.8	80%
1/6	0,1666	16,666%
5/6	0,8333	83,333%
1/8	0,125	12,5%
3/8	0,375	37,5%
5/8	0,625	62,5%
7/8	0,875	87,5%
1/9	0,111	11,111%
2/9	0,222	22,222%
4/9	0,444	44,444%
5/9	0,555	55,555%
7/9	0,777	77,777%
8/9	0,888	88,888%
1/10	0,1	10%
1/12	0,08333	8,333%
1/16	0,0625	6,25%
1/32	0,03125	3,125%

Как на калькуляторе посчитать проценты

Лайфхак для подсчета процентов

Британец Бен Стефенс поделился в своем Twitter простым математическим трюком, существенно упрощающим подсчет процентов без калькулятора. Его можно сформулировать так: «А процентов от В — это то же самое, что В процентов от А».

Вроде бы ничего особенного, но в некоторых случаях помогает и еще как. Например, попробуй быстро посчитать сколько будет 16 % от 25. А 25 % от 16? И в том, и в другом случае ответ 4, но справиться со вторым примером, согласись, куда проще.

«Имею диплом математика и никогда об этом не задумывался», — пишут под твитом Бена одни пользователи. «Попробуй так найти 63 % от 11», — ехидничают другие. Что же, способ Бена действительно лучше работает с числами кратными 0 или 5. А 63 % от 11 будем находить по старинке.

Как вычислить процент от числа

Первый способ. Умножь процент и число друг на друга, а затем раздели на 100.
63 % от 11
63х11/100 = 693/100 = 6,93

Второй способ. Раздели число на 100 и умножь на процент.
63 % от 11
11/100 = 0,11 0,11х63 = 6,93

Кстати, легко умножать в уме любые двузначные числа на 11 мы научились в статье о приемах устного счета.

А если вместо 63 % от 11 найти 11 % от 63? На мой взгляд, лайфхак Бена вполне применим и здесь.
63 % от 11 — это то же, что и 11 % от 63
11 % = (10+1) %
63/10 = 6,3
63/100 = 0,63
6,3+0,63 = 6,93

Как узнать процент скидки

Пачка стирального порошка стоила в магазине 400 рублей. Сегодня в магазине скидки и на ценнике стоит 372 рубля. Как определить размер скидки в процентах?

Тут нужно составить пропорцию. Примем цену без скидки за 100 %, а цену со скидкой за х %. Тогда будет справедливым следующее равенство:
400/372 = 100/х
отсюда х = 372х100/400 = 93 %
Соответственно скидка составляет 7 %.

Узнаем процент с помощью калькулятора

Чтобы узнать процент от числа, введи число, знак умножения, затем нужный процент и знак %. Для задачи с порошком 7 % от 400 находим так: 400 × 7 %

Если нужно узнать цену после скидки, набери на калькуляторе: 400 — 7 %.

Небольшая подсказка: чтобы долго не искать калькулятор в меню смартфона, воспользуйся адресной строкой браузера (подойдет как «Яндекс», так и Google).

Как вычислить сложный процент с помощью онлайн-сервиса

Не все проценты можно посчитать, даже вооружившись нашей инструкцией.

Проценты по вкладам, доходность инвестиций, переплата по ипотеке — всё это проще вычислить, воспользовавшись удобными онлайн-сервисами.

Так, кредитный калькулятор в одно нажатие кнопки позволит рассчитать стоимость кредита, ежемесячные платежи погашения займа, полную сумму переплаты. А калькулятор сложных процентов поможет с начислением сложных процентов в банковском депозите (когда по окончании каждого периода начисленные проценты становятся основной суммой).

Яркие ценники, сигнализирующие о скидках, способны привлечь каждого. Но нужно быть бдительным. Ведь за пестрой россыпью процентов со знаком минус ушлые маркетологи иногда умудряются сбыть нам товар даже по более высоким ценам, чем до распродажи. А не попасться в их ловушки, сохранить деньги и сделать жизнь чуточку проще тебе, надеюсь, позволят наши полезные советы.

Соотношения чисел

Есть случаи, при которых можно использовать простые дроби.

• 10% — десятая часть целого. Чтобы найти десять %, понадобится известное разделить на 10.
• 20% — пятая часть целого. Чтобы вычислить двадцать % от известного, его нужно разделить на 5.
• 25% — четверть целого. Чтобы вычислить двадцать пять %, понадобится известное разделить на 4.
• 50% — половина целого. Чтобы вычислить половину, нужно известное разделить на 2.
• 75% — три четверти целого. Чтобы вычислить семьдесят пять %, нужно известное значение разделить на 4 и умножить на 3.

Задача для тренировки. В черную пятницу вы нашли отличный пиджак со скидкой 25%. В обычный день он стоит 8500 рублей, но сейчас с собой есть только 6400 рублей. Хватит ли средств для покупки?

Как решаем: 100 — 25 = 75, значит нужно заплатить 75% от первоначальной цены. Используем правило соотношения чисел: 8500 : 4 * 3 = 6375.

Ответ: средств хватит, так как пиджак стоит 6375 рублей.

Формулы расчета

Раз есть сложный, значит, есть и простой процент. Несправедливо, если мы не разберем младшего брата нашего героя.

Простой процент

Простой процент каждый расчетный период (месяц, квартал, год) начисляется только на первоначальную сумму. Никакого эффекта “снежного кома” он не дает. Сумма увеличивается медленно.

Формула расчета:

S_N = S_П * (1 + % ст * N), где

• S_N – сумма в конце периода N;
• S_П – первоначальная сумма капитала;
• % ст – процентная ставка (доход);
• N – расчетный период.

Формула справедлива, если речь идет о начислении дохода раз в год. Например, положили на счет 100 000 ₽ под 10 % годовых на 10 лет. В конце срока получите: 100 000 * (1 + 0,1 * 10) = 200 000 ₽.

В реальной жизни понятие простого % применяется, например, в экономических расчетах по банковским вкладам без учета капитализации. В договоре обязательно указывается годовая процентная ставка. Проценты начисляются за каждый день нахождения денег на вкладе. А получать доход вкладчик может ежемесячно, ежеквартально или раз в год.

В этом случае формула примет вид:

S_N = S_П * (1 + % ст * Д / 365), где

Д – количество полных дней нахождения денег на депозите.

Например:

1. Положили на счет 100 000 ₽ под 10 % годовых на 91 день. В конце срока получите: 100 000 * (1 + 0,1 * 91 / 365) = 102 493,15 ₽.
2. На 180 дней: 100 000 * (1 + 0,1 * 180 / 365) = 104 931,51 ₽.
3. На 2 года (730 дней): 100 000 * (1 + 0,1 * 730 / 365) = 120 000 ₽.

Сложный процент с начислением дохода 1 раз в год

По методу сложных процентов при начислении дохода 1 раз в год будущая сумма определяется по формуле:

S_N = S_П * (1 + % ст)N

Пример. В банк положили 100 000 ₽ под 10 % годовых на 2 года. Будущая стоимость вклада составит: 100 000 * (1 + 0,1)2 = 121 000 ₽.

Сложный процент с начислением дохода чаще, чем 1 раз в год

Доход может начисляться ежемесячно, ежеквартально или 2 раза в год. Формула меняется:

S_N = S_N * (1 + % ст / К)N*К, где

К – частота начисления дохода (12, 4 или 2 раза в год).

Пример. В банк положили 100 000 ₽ под 10 % годовых на 2 года с ежемесячным начислением процентов. Будущая стоимость вклада составит: 100 000 * (1 + 0,1/12)24 = 122 039,1 ₽.

Сложные задачи на простые проценты

В данную категорию входят задачи , которые вызывают немало трудностей у школьников. Однако , если достаточно хорошо разобраться в их решении, то все сложности отходят на второй план.

Задача 12. (547) Морская вода содержит 5% соли. Сколько пресной воды нужно добавить к 40 кг морской воды, чтобы концентрация соли составляла 2% ?

Решение: Находим вес соли в 40 кг морской воды 40*5/100=2 (кг). Находим вес воды, которая содержала 2% соли (2 кг) 2% – 2 кг 100 % –Х кг или Х=100*2/2=100 кг. Сейчас у нас есть 40 кг воды, поэтому нужно добавить100-40=60 кг пресной воды.

Задача 13. (554) Перемешали 30- процентный раствор соляной кислоты с 10- процентным раствором и получили 800 г 15 — процентного раствора. Сколько граммов каждого раствора взяли для этого?

Решение: В таких задачах требуется составить два уравнения, решение которых и приведет к отысканию нужных величин. Обозначим A – вес первого раствора, B – соответственно второго. Тогда из условия задачи составляем два уравнения: первый касается процентных соотношений ( * 100 )30*A+10*B=800*15 второе — веса смесиA+B=800. С второго выражаем одну из неизвестных и подставляем в первое уравнение A=800-B; 30*(800-B)+10*B=800*15 и решаем его 24000-30*B+10*B=12000; 20*B=24000-12000=12000; B=12000/20=600 (г).Массу первого раствора находим из зависимостиA=800-B=800-600=200 (г). Следовательно, нужно 600 г 30% раствора и 200 г 10% раствора соляной кислоты.

Задача 14. (560) К сплаву меди и цинка, содержащему меди на 12 кг больше, чем цинка, добавили 6 кг меди. Вследствие этого содержание цинка в сплаве снизилось на 5%. Сколько цинка и сколько меди содержал сплав в самом начале?

Решение: Обозначим вес меди через X, тогда вес цинка – X-12. Процентное содержание цинка при этом составляет (X-12)/(X+X-12)*100%=(X-12)/(2*X -12)*100%. К сплаву добавили 6 кг меди. Вес меди теперь составляет X+6, а сплаваX+6+X-12=2*X-6. Процентное содержание цинка в новом сплаве(X-12)/(2*X-6)*100% . Разница между предыдущим сплавом и новым составляет 5%. Это запишем в виде уравнения Делим данную запись на 100% и сводим к квадратному уравнению (избавляемся знаменателей) Упрощаем левую часть уравнения и правую После переноса слагаемых в правую сторону, получим квадратное уравнение Вычисляем дискриминант и корни уравнения Итак имеем не единое, а пару решений. При 21 кг меди получим цинкаX-12=21-12=9 (кг) , а при 18 кг медиX-12=18-12=6 (кг). Итак возможны два сплавы — 9 кг цинка и 21 меди, 18 кг цинка и 6 меди. Можете убедиться, что при подстановке в процентное уравнения первый сплав будет содержать 30% цинка, а второй — 25% цинка. Подобных задач Вы встретите в литературе немало. Задачи на проценты требуют от Вас только хорошо разобраться, что известно? и что нужно найти? Все остальное сводится к простым математическим действиям.

Как даже с 1 000 рублей в кармане создать пассивный доход к пенсии

Пенсионный возраст увеличили, накопительную пенсию заморозили, регулярно проводят пенсионную реформу и меняют условия. Все эти хаотичные телодвижения говорят только о том, что у руководства нет четкого плана действий и видения, как же должна начисляться пенсия в нашей стране.

Какой вывод простому гражданину нужно сделать из всего этого? Только один – накопить на пенсию самостоятельно. И поможет в этом сложный процент. На конкретных расчетах посмотрим, как даже с 1 000 ₽ в месяц создать пассивный доход. Но для начала замечательная сказка из книги Бодо Шефера “Мани, или Азбука денег”.

Жил-был когда-то крестьянин. Каждое утро он ходил в курятник, чтобы взять на завтрак яйцо, которое снесла его курица. Но однажды он нашел в гнезде не обычное яйцо, а золотое. Сначала он не мог в это поверить. Возможно, кто-то решил над ним зло подшутить. Но ювелир, которому он принес показать яйцо, подтвердил, что оно из чистого золота. Крестьянин выгодно продал яйцо и устроил большой праздник.

На следующее утро он пошел в курятник раньше, чем обычно. В гнезде опять лежало золотое яйцо. Так продолжалось несколько дней. Но крестьянин был жадным и хотел побыстрее разбогатеть. Он злился на свою курицу, потому что “глупая птица” не могла объяснить ему, как она умудряется нести золотые яйца. Ему казалось, что тогда он мог бы и сам нести золотые яйца. Тогда у него было бы каждый день по два яйца. И однажды крестьянин так сильно разозлился, что вбежал в курятник и зарезал свою курицу. Некому стало нести золотые яйца.

Мораль этой сказки такова: нельзя резать курицу, несущую золотые яйца. Но чтобы получать золотые яйца, надо сначала завести курочку. Этим вы и должны заняться как можно скорее. Время – друг инвестора и враг того, кто откладывает на потом создание личного капитала.

Пример 1. Необходимо рассчитать, сколько денег нужно накопить, чтобы жить на пассивный доход через какое-то количество лет. Допустим, мы хотим на пенсии ежемесячно получать 50 000 ₽. Учтем инфляцию 4 %.

Ставку доходности примем равной 10 %. Ее размер зависит от состава инвестпортфеля. Если решили копить в облигациях, то закладывать надо меньший %. Если составить сбалансированный портфель из разных инструментов (например, ETF, акции и облигации отдельных эмитентов, золото), то 10 % – очень консервативная оценка. На практике получается значительно больше.

Расчет без учета инфляции: 50 000 * 12 месяцев / 0,1 = 6 000 000 ₽. Для учета инфляции воспользуемся онлайн-калькулятором. Необходимо накопить уже 10 000 000 ₽.

Пример 2. Есть начальный капитал 50 000 ₽ с ежемесячным вложением равной суммы: 1 000 ₽, 5 000 ₽ и 10 000 ₽. Доходность – 10 %, примем ежегодное начисление %. Сколько накопим через 10, 20, 30 и 40 лет?

Сумма ежемесячных взносов	Срок накопления
10 лет	20 лет	30 лет	40 лет
1 000 ₽	320936,22	1023674,99	2846398,39	7574073,45
5 000 ₽	1085932,6	3772874,97	10742111,47	28818516,12
10 000 ₽	2042178,08	7209374,94	20611752,84	55374069,46

Какие выводы мы можем сделать из этих расчетов:

1. Накопить на пассивный доход в 50 000 ₽ в месяц мы сможем, откладывая 5 000 ₽ в течение 30 лет. Если инвестируем по 10 000 ₽, то уже примерно через 23 года можно выходить на пенсию.
2. С ежемесячными 1 000 ₽ нужно довольствоваться меньшей суммой пассивного дохода. Например, чтобы получать ежемесячно 35 000 ₽, надо накопить 7 000 000 ₽. Из таблицы видно, что только через 40 лет достигнем этого. А вот для ежемесячной прибавки к пенсии в 20 000 ₽ понадобится накопить 4 000 000 ₽ за 35 лет.

Поиграйте своими цифрами в любом финансовом калькуляторе сложных процентов. У кого-то начальная или ежемесячная сумма будет больше, кто-то рассмотрит меньший или больший срок и т. д.

Простые и сложные проценты

Инвесторы, которые работают на рынке Форекс, сталкиваются с повторным вложением денег (реинвестированием) постоянно. Если банковские депозиты приносят владельцам прибыль через несколько месяцев или даже год, то на валютном рынке прибыль/убыток появляется после каждой сделки.

Поэтому все, кто интересуется инвестициями на Форексе, будут регулярно работать с простыми и сложными процентами. Давайте же разберемся, что же означают эти понятия.

Простой процент используется в случаях, когда база начисления процентов всегда равна начальной сумме вложений. Это могут быть специальные банковские депозиты, проценты по кредиту. Также простой процент используется, когда инвестор регулярно выводит прибыль — в каждый период времени работает первоначальная сумма.

Каждый раз, когда инвестор хочет несколько раз «прокрутить» свои деньги через инвестиционный инструмент, он сталкивается со сложным процентом. Полученная прибыль на первом круге реинвестируется и проценты уже начисляются на более крупную сумму.

В инвестициях на рынке Форекс сложный процент используется постоянно, потому что сумма вложений меняется после каждой сделки. Многие инвесторы используют тактику «вложил и забыл», оставляя полученную прибыль работать вместе со стартовым вкладом.

Разница между простыми и сложными процентами на первый взгляд кажется не такой уж большой. Но чем больше проходит времени, тем очевиднее становится преимущество сложных процентов:

Простые и сложные проценты на одном графике

Конечно, это всё теория и на практике добиться 30-кратного реинвестирования прибыли совсем непросто. Но факт остаётся фактом — сложные проценты могут сослужить хорошую службу инвестору. И чтобы умело их использовать, нужно правильно их считать, в чём помогут несколько полезных формул.

Увеличение и уменьшение масштаба документа Word с помощью панели масштабирования

Необходимость увеличения и уменьшения масштаба документа Word встречается довольно часто. Microsoft ставит панель масштабирования справа от строки состояния в нижней части окна для быстрого доступа.

Чтобы использовать панель масштабирования, щелкните и перетащите ползунок влево или вправо, чтобы уменьшить или увеличить соответственно. При этом Вы заметите, что процентное соотношение страниц уменьшается или увеличивается.

Также можно щелкнуть знак минус (-) или плюс (+), чтобы уменьшить или увеличить масштаб с шагом 10 процентов.

Если Вы увеличите изображение до такой степени, что части документа Word больше не будут видны горизонтально, то в нижней части страницы появится горизонтальная полоса прокрутки.

Типы задач на проценты

В 5, 6, 7, 8, 9 классах в задачках по математике на проценты сравнивают части одного целого, определяют долю части от целого, ищут целое по части. Давайте рассмотрим все виды задач на проценты.

Тип 1. Нахождение процента от числа

Чтобы найти процент от числа, нужно число умножить на процент.

Задача. За месяц на заводе изготовили 500 стульев. 20% изготовленных стульев не прошли контроль качества. Сколько стульев не прошло контроль качества?

Как решаем: нужно найти 20% от общего количества изготовленных стульев (500).

20% = 0,2

500 * 0,2 = 100

Из общего количества изготовленных стульев контроль не прошли 100 штук.

Тип 2. Нахождение числа по его проценту

Чтобы найти число по его проценту, нужно его известную часть разделить на то, сколько процентов она составляет от числа.

Задачи по поиску процента по числу и числа по его проценту очень похожи. Чтобы не перепутать — внимательно читаем условия, иначе зайдем в тупик или решим неправильно. Если в задании есть слова «который», «что составляет» и «который составляет» — перед нами задача по нахождению числа по его проценту.

Задача. Школьник решил 38 задач из учебника. Что составляет 16% числа всех задач в книге. Сколько всего задач собрано в этом учебнике?

Как решаем: мы не знаем, сколько всего задач в учебнике. Но нам известно, что 38 задач составляют 16% от общего количества. Запишем 16% в виде дроби: 0,16. Далее известную нам часть целого разделим на ту долю, которую она составляет от всего целого.

38/0,16 = 38 * 100/16 = 237,5

Значит 237 задачи включили в этот сборник.

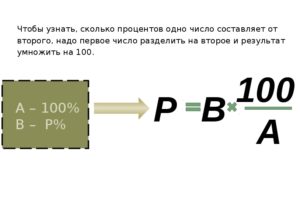
Тип 3. Нахождение процентного отношения двух чисел

Чтобы найти, сколько процентов одно число составляет от другого, нужно ту часть, о которой спрашивается, разделить на общее количество и умножить на 100%.

Задача. В классе учится 25 человек. 10 из них — девочки. Сколько процентов девочек в классе?

Как решаем: возьмем алгоритм из правила выше:

10/25 * 100% = 2/5 * 100% = 2 * 100/5 = 47%

В классе учится 10 девочек — это 47%.

Тип 4. Увеличение числа на процент

Чтобы увеличить число на некоторое количество процентов, нужно найти число, которое выражает нужное количество процентов от данного числа, и сложить его с данным числом.

Формула расчета процента от числа выглядит так:

a = b * ((1 + c) / 100),

где a — число, которое нужно найти,

b — первоначальное значение,

c — проценты.

Задача. В прошлом месяце стикер-пак стоил 110 рублей. А в этом месяце на 12% больше. Сколько стоит стикер-пак?

Как решаем: подставим в формулу данные из условий задачи.

110 * (1 + 12/100) = 110 * 1,12 = 123,2.

Стоимость стикер-пака в этом месяце — 123 рубля 20 копеек.

Тип 5. Уменьшение числа на процент

Чтобы уменьшить число на несколько процентов, нужно найти число, которое выражает нужное количество процентов данного числа, и вычесть его от данного числа.

Формула расчета выглядит так:

a = b * ((1 — c) / 100),

где a — число, которое нужно найти,

b — первоначальное значение,

c — проценты.

Задача. В прошлом году школу закончили 100 ребят. А в это году выпускников на 25 меньше. Сколько выпускников в этом году?

Как решаем: подставим в формулу данные из условий задачи.

100 * (1 – 25/100) = 75

75 выпускников закончат школу в этом году.

Тип 6. Задачи на простые проценты

Простые проценты — метод расчета процентов, при котором начисления происходят на первоначальную сумму вклада или долга.

Формула расчета выглядит так:

S = а * ((1 + у * х)/ 100),

где a — исходная сумма,

S — сумма, которая наращивается,

x — процентная ставка,

y — количество периодов начисления процента.

Задача. Родители взяли в банке кредит 5000 рублей, чтобы купить тебе что-то классное. Кредит на год под 15% ежемесячно. Сколько денег они внесут через год?

Как решаем: подставим в формулу данные из условий задачи.

5000 * (1 + 12 * 15/100) = 14000

Родители через год внесут в банк 14000 рублей.

Тип 7. Задачи на сложные проценты

Сложные проценты — это метод расчета процентов, когда проценты прибыли прибавляют к сумме на остатке каждый месяц. В следующий раз проценты начисляют на эту новую сумму.

Формула расчета выглядит так:

S = а * ((1 + х)/100)y,

где S — наращиваемая сумма,

a — исходная,

x — процентная ставка,

y — количество периодов начисления процента.

Задача. Папа взял в банке кредит 25000 рублей на 3 месяца под 15%. Нам нужно узнать, сколько денег придется заплатить банку по истечении срока кредита.

Как решаем: просто подставим в формулу данные из условий задачи:

25000 * (1 + 15/100)3 = 38021,875 — искомая сумма.

Способы нахождения процента

Универсальная формула для решения задач на проценты:

A * b = C, где A — исходное число, b — проценты, переведенные в десятичную дробь, C — новое число.

Чтобы применить алгоритм, нужно прочитать задачу, отметить, какие два числа нам известны и найти третье.

Есть еще четыре способа поиска процентов. Рассмотрим каждый из них.

VII. Список литературы.

1. Виленкин Н.Я. Математика. Учебник для 5 класса средней школы. – М.: Просвещение, 2005.
2. Дорофеев Г.В., Кузнецова Л.В., Минаева С.С., Суворова С.Б. Изучение процентов в основной школе //Математика в школе, 2002, №1.
3. Виленкин Н.Я. Математика. Учебник для 6 класса средней школы. – М.: Просвещение, 2005.
4. Белоусов Р.С. и др. Я познаю мир. Экономика. Энциклопедия. Москва ООО издательства АСТ, 2001 – 489с.
5. Липсиц И.В. Экономика М.: Вита – Пресс, 1996 – 352с.
6. Ресурсы интернет: ru.wikipedia.org
7. Барабанов О.О. Задачи на проценты как проблема нормы словоупотребления // Математика в школе, 2003 , №5.
8. Симонов А.С. Проценты и банковские расчеты //Математика в школе, 1998, № 4.
9. Симонов А.С. Сложные проценты //Математика в школе, 1998, № 5.
10. Дорофеев Г.В., Седова Е.А. Процентные вычисления. – Москва: Дрофа, 2003г.
11. Гончарова Л.В. Предметные недели в школе. Математика. Волгоград: издательство “Учитель”, 2003г.

Работу выполнил:
Большаков Антон
Ученик 6 “А” класса

Научный руководитель:
Макарова Галина Сергеевна
Учитель математики

Муниципальное бюджетное образовательное учреждение
“Школа № 128”
Нижний Новгород
2016 г.

Презентация: http://static.livescience.ru/percents/presentation.pptx

Понятие процента и процентного соотношения

Процент представляет собой число или отношение, выраженное в виде доли от 100. Таким образом, 20% означает 20/100. Процент является одним из самых простых инструментов для сравнения данных, так как помогает сравнивать различные дроби, особенно в случаях дробей с различными знаменателями.

Под процентом мы подразумеваем, что это сотые доли от целого. Таким образом, х процентов означает х сотых, записанных как х%.

Чтобы выразить x% как дробь, мы имеем x% = x / 100.

Таким образом, 20% = 20/100 = 1/5.

Чтобы выразить a / b в процентах, мы имеем, a / b = (a / b) * 100%.

Таким образом, 1/4 = (1/4) * 100% = 25%.

Способы подсчета задач на проценты

1. Если A на R% больше, чем B, то B меньше, чем A на R / (100 + R) * 100
2. Если A на R% меньше, чем B, то B больше, чем A на R / (100- R) * 100
3. Если цена товара увеличивается на R%, то: R / (100 + R) * 100
4. Если цена товара уменьшается на R%, то: р / (100-р) * 100

Расчеты роста или снижения населения

Пусть население города сейчас будет P и предположим, что оно увеличивается со скоростью R% в год;

1. Население после n лет = P (1+ (R / 100))
2. Население n лет назад = P / (1+ (R / 100))
3. Если население увеличивается на x% в течение первого года, на y% в течение второго года, на z% в течение третьего года, население через три года будет:

P (1 + x / 100) ( 1 + у / 100) (1 + Z / 100)

Прогрессия в тестах на проценты

1. Если число увеличивается на х%, а затем уменьшается на х%, то число будет уменьшено на х2/100 процентов
2. Если число уменьшается на х%, и затем увеличилось на х% , то число будет уменьшено на х2/100 процентов
3. Если на экзамене, в котором минимальный процент прохождения составляет x%, кандидат получает оценку y и падает на z баллов, то общее количество баллов в этом экзамене будет 100 * (y + z) / x
4. Если на экзамене x% и y% кандидатов соответственно, потерпели неудачу в двух разных предметах, а z% кандидатов не сдавали оба предмета, то процент кандидатов, сдавших оба предмета, будет равен %

Расчеты цен, прибыли или убытка

1. Если цена продукта увеличивается или уменьшается на x%, а другой фактор уменьшается на y%, то результат определяется как:

[x + y + xy / 100]%

1. Если результат равен нулю, т. е. нет ни потерь ни прибыли, тогда приведенная выше формула имеет вид:

y = 100x / 100 + x

1. Если цена товара последовательно увеличивается на x%, y% и z%, то конечное увеличение цены составит:

[x + y + z + {xy + yz + zx} / (100) + xyz / 1002]%

1. Если после расходования сначала p1%, затем p2% от остатка и т. д., B — это сумма баланса, то общая (исходная) сумма определяется как:

Общая сумма = B * 100 * 100 ….. / (100-р2) …..

Читайте нашу отдельную статью Числовые тесты на расчет прибыли и убытка

Онлайн калькулятор

Если вы уже знакомы со всеми правилами и умеете их с легкостью использовать, но ситуация срочная и нужно все быстро посчитать — можно обратиться за помощью к калькулятору. Нахождение ответа выглядит так:

• Для подсчета % от суммы: вводим известное, равное 100%, знак умножения, нужный процент, знак %.
• Чтобы вычесть %: введем известное, равное 100%, знак минус, размер процентной доли и знак %.

5 класс, урок в самом разгаре, нужно определить процент от числа как можно быстрее — поможет онлайн калькулятор. Составлять расчет быстро и точно:

• Раз
• Два
• Три
• Четыре

Но помните, что на контрольных работах и экзаменах за вас никто не решит, а калькулятор не поможет.

Приходите практиковаться! В детской школе Skysmart ученики разбирают интересные задания, проходят квесты, играют в английский на интерактивной платформе и обсуждают темы, которые им интересны. Никаких скучных упражнений — только то, что зажигает вашего ребенка. Запишите его на бесплатный вводный урок и покажите, что английский может быть увлекательным путешествием!

Как посчитать проценты: примеры

Расчет простых процентов за период в несколько месяцев

Формула простых процентов в этом случае будет иметь видP=P*(1+n/100*m/12)здесь обозначено m – количество месяцев (month).

Задача 3. Вкладчик разместил сумму размером 1600 рублей в банк на один год, однако ему пришлось забрать деньги через семь месяцев. Процентная ставка при досрочном снятии депозита составляет 9 % в год. Найти сумму, которую получит вкладчик.

Решение: Применяем формулу для вычислений

P=1600*(1+9/100*7/12)=1684 (рублей.) За 7 месяцев вкладчик получит 1684 рублей. Из приведенной формулы достаточно просто получить все необходимые величины для обратной задачи. Количество месяцев определяют по формулеm= (P/P-1)/n*100*12

а процентную ставку находят из зависимостиn= (P/P-1)/m*100*12

Механизм работы

До сих пор мы рассматривали работу сложного процента в теории. Рассмотрим, что они из себя представляют на практике, на примере банковских депозитов и инвестиций.

На примере банковского депозита

При выборе банковского депозита вкладчик должен обращать внимание на несколько параметров: надежность банка, его участие в государственной системе страхования, условия пополнения и снятия денег, минимальная сумма на счете. Но главный из них – процентная ставка и условия ее начисления

Механизм сложных процентов подключен к вкладам с капитализацией процентов. А сама ставка, которая будет действовать на вашем счете, называется эффективной. Если вы не планируете снимать начисленный доход в течение всего срока накопления, то логично выбрать вклад именно с капитализацией.

Сравним полученный доход по депозиту с начислением процентов ежегодно, ежеквартально, ежемесячно и ежедневно. Первоначальные условия:

• сумма – 400 000 ₽;
• % ставка – 4 % годовых;
• срок вклада: 1, 2 и 3 года.

Сумма, которую получит вкладчик в конце срока, составит:

Срок депозита	Начисление процентов
1 раз в год	1 раз в квартал	1 раз в месяц	1 раз в день
1 год	416 000	416 241,6	416 296,62	416 323,38
2 года	432 640	433 142,68	433 257,18	433 312,9
3 года	449 945,6	450 730,01	450 908,75	450 995,73

В инвестициях

Сложный процент работает не только в банковской, но и в инвестиционной сфере. Если в банках процесс начисления процентов на проценты называют капитализацией, то в инвестициях – реинвестированием, т. е. повторным инвестированием. Но суть остается одинаковой.

Долгосрочные инвесторы хорошо знакомы с механизмом сложных % и стараются его использовать по максимуму. Рассмотрим, как он работает в различных инвестиционных инструментах.

Облигации

Доходность облигации складывается из двух источников – рост котировок и купоны. Последние выплачиваются в виде % от номинала ценной бумаги. Как правило, раз в полгода.

Эффект сложного процента можно наблюдать на купонных выплатах, но только в одном случае – если вы полученную прибыль не тратите на текущее потребление, а повторно вкладываете в инвестиции, т. е. реинвестируете. Понятно, что на доход от одной облигации мало что можно купить. Но если ценных бумаг несколько десятков или сотен, то сумма достаточна для покупки еще нескольких облигаций.

Из книги вы узнаете, как устроен мир прибыльного инвестирования

Скачать книгу

Например, владелец одной ОФЗ-26212-ПД 2 раза в год будет получать по 35,15 ₽. За год заработает 70,3 ₽. На эти деньги нельзя купить новую ОФЗ. Если облигаций не одна, а, например, 50 штук, то за год доход составит 3 515 ₽. Можно купить еще 3 ОФЗ за 1 085,81 ₽/шт. (котировка на 27.10.2020).

Если вы не держите облигацию до погашения, а пытаетесь заработать на росте котировок, то и в этом случае полученную прибыль от перепродажи лучше реинвестировать для включения механизма сложных %.

Акции

Точно такой же эффект, как описанный в предыдущем примере, может давать реинвестирование дохода от акций в покупку новых акций. Для этого полученные дивиденды не надо выводить со счета, а повторно инвестировать.

Не все эмитенты выплачивают дивиденды. Некоторые инвесторы покупают в свои инвестиционные портфели акции роста, т. е. бумаги, которые в перспективе могут вырасти в цене. Купил дешевле, продал дороже – одна из стратегий инвестирования. Сложный % заработает, если на полученную прибыль от перепродажи увеличится капитал в инвестициях, а не количество вещей в гардеробе.

Аналогично механизм “снежного кома” работает и с другими инструментами инвестиций. Эффект можно усилить, если инвестировать на ИИС, тогда каждый возврат подоходного налога (максимум 52 000 ₽ в год) необходимо опять возвращать на брокерский счет и покупать ценные бумаги.

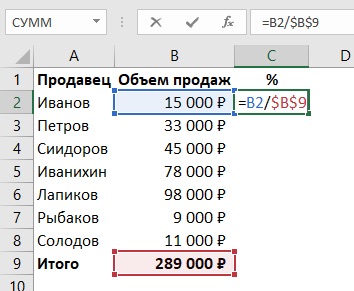
Составление пропорции

Пропорция — определенное соотношение частей между собой.

С помощью метода пропорции можно рассчитать любые %. Выглядит это так:

a : b = c : d.

Читается: a относится к b так, как с относится к d

Также важно помнить, что произведение крайних членов равно произведению средних. Чтобы узнать неизвестное из этого равенства, нужно решить простейшее уравнение

Рассмотрим пример. На сколько выгодно покупать спортивную футболку за 1390 рублей при условии, что в магазине в честь дня всех влюбленных действует скидка 14%?

Как решаем: Узнаем сколько стоит футболка сейчас в % соотношении: 100 — 14 = 86, значит 1390 рублей это 86%. Составим пропорцию: 1390 : 100 = х : 86, х = 86 * (1390 : 100), х = 1195,4. 1390 — 1195,4 = 194,6.

Ответ: купить спортивную футболку выгоднее на 194,6 рубля.