Сложение, вычитание, умножение и деление в excel

1.3. Адресация

A1C5Name BoxA1F=адрес=A1

Например, первая ячейка имеет абсолютный адрес –  $A$1, относительный адрес –
A1, и два
смешанных адреса – $A1 и
A$1. Различие в способе адресации проявляется,
прежде всего, тогда, когда формула копируется и переносится в другое
место. Поясним это на простом примере.

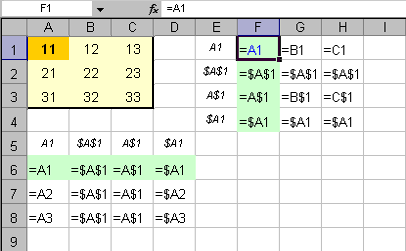
Рис. 5 Абсолютная и относительная адресация

На верхней панели показан фрагмент листа с
данными, выделенными желтым цветом. В зеленых областях (столбец
F и строка 6)
приведены различные варианты адресации одной и той же ячейки –
A1 (выделена оранжевым). Тип адресации
указан рядом с соответствующей ячейкой. Скопируем каждую из зеленых
областей (по очереди) и вставим рядом – в соседних столбцах:
G и H, и в
соседних строках: 7 и
8 (средняя панель ). Видно, что
результат зависит от типа адресации. Для абсолютной адресации ссылка на
первую ячейку сохранилась. Для относительной – ссылка сдвигается вправо
или вниз, сохраняя относительное положение двух ячеек: той, где стоит
ссылка, и той, на которую ссылаются. Для смешанной адресации результат
зависит от того, куда переносится копия, и от того, какая часть адреса
фиксируется значком доллара $. На правой
панели показаны соответствующие формулы, получающиеся после копирования.
Заметим, что ссылки на ячейки могут изменяться в зависимости от способа
адресации, но при перемещении ячейки с формулой содержащиеся в формуле
ссылки не изменяются.

Для адресации ячейки, которая находится на другом листе той же книги,
надо указывать еще и имя листа, например: Data!B2.
Восклицательный знак (!) отделяет имя листа
от адреса ячейки. Если имя листа содержит пробел, тогда имя надо
заключить в одинарные кавычки, например ‘Raw
Spectra’!C6. При адресации к другой книге, ее имя указывается
впереди, в квадратных скобках, например;
Results!P24

Подробнее о способах адресации можно прочитать

здесь.

Способ 1: Специализированные приложения

Существует довольно много программ, предоставляющих возможность скрытия папок и файлов, а также их защиты путем установки кодовой комбинации. Воспользуемся одним из них для решения нашей сегодняшней задачи.

1. Скачайте приложение с официального сайта, воспользовавшись представленной выше ссылкой. Установите его на свой компьютер и запустите. Придумайте и дважды введите пароль, который будет использоваться для защиты непосредственно Wise Folder Hider.

2. В главном окне перейдите во вкладку «Зашифровать файл» и нажмите по расположенной внизу кнопке «Создать».

Определите параметры создаваемого файла, который на деле будет представлять собой виртуальный диск для хранения данных. Задайте ему имя, укажите папку расположения, выберите размер (в бесплатной версии – не более 50 Мб, но для текстового документа этого более чем достаточно), затем нажмите «Создать».

Спустя несколько секунд в окне программы появится созданный виртуальный файл, параллельно с этим в «Проводнике» будет открыто его расположение. Именно в эту директорию и следует поместить документ Word, который вы хотите защитить паролем. Скопируйте и вставьте его сюда или переместите из изначальной папки.

Далее в колонке «Операция» нажмите на указывающий вниз треугольник, чтобы вызвать выпадающий список, и выберите пункт «Установить пароль».

Дважды введите кодовое выражение, которое хотите использовать для защиты текстового файла Ворд и содержащего его виртуального диска. Нажмите «ОК» для подтверждения,

а затем еще раз, чтобы «Задать пароль».

В дальнейшем открыть созданную с помощью Wise Folder Hider папку можно будет через «Этот компьютер», где она отображается в виде одного из накопителей.

Если же в этом перечне диск будет отсутствовать, его потребуется добавить через интерфейс самой программы. В уже знакомой нам колонке «Операция» следует нажать по кнопке «Монтировать», ввести установленный на предыдущем шаге пароль и кликнуть «ОК» для подтверждения. Повторное нажатие кнопки (когда она называется «Размонтировать») скроет накопитель из «Проводника».

Как уже было сказано выше, рассмотренный нами Wise Folder Hider – далеко не единственное программное средство для установки защитной комбинации на папки и файлы. К тому же большинство из них предоставляют еще одни вариант решения нашей сегодняшней задачи – вместо шифрования файла и создания виртуального диска можно поместить требующие защиты данные в отдельную директорию и поставить пароль на нее.

Подробнее:Программы для защиты файлов и папокКак поставить пароль на папку в Windows

3.3. Пример макроса

Второй способ опирается на рекуррентное соотношение,
связывающее два соседних члена в ряду  

Для того чтобы воспользоваться этим соотношением, надо
организовать на листе рекуррентную процедуру. Например, так, как
показано на Рис. 42  

Рис.42 Вычисление функции E₁(x)
итерационным способом

Один шаг итерации – это переход от значений в области
J2:J4 к значениям в области
L2:L4. Для того, чтобы сделать следующую
итерацию, нужно скопировать значения, получившиеся в области
L2:L4 и вставить их в область
J2:J4. При этом вставлять нужно только
величины, без формул. Величины в области H2:H4
дают исходные значения для начала итерации .Повторяя многократно
операцию Copy-Paste Special, можно получить в
ячейке L4 искомое значение. Однако
копирование – это скучное занятие и его было бы неплохо
автоматизировать. Для этого можно написать макрос.

Проще всего начать создание макроса через запись команд,
выполняемых на листе. Для этого идем в раздел меню Tools–Macro–Record
New Macro. Появляется окно (Рис. 43), в котором можно указать имя
макроса и где он будет расположен.  

Рис.43 Запись макро

После нажатия OK начинается
запись всех действий, выполняемых на листе. Когда все, что нужно
сохранено в макросе, запись надо остановить командой
Tools–Macro–Stop Recording. Результат можно увидеть, зайдя в
.   

 

Рис.44 Редактор Visual Basic

На Рис. 44 показан записанный макрос, который мы подвергли
небольшому редактированию – добавили цикл для повтора операции
Copy-Paste в числе nIter
раз. Величина nIter берется со
страницы из ячейки J6,
имеющей локальное имя n. Завершает
автоматизацию кнопка Repeat, к которой
привязан макрос Iteration.  

Такой подход использовался нами для построения
алгоритмов и в многомерном разрешении кривых.

Определение умножения

Рассмотрим две согласованные матрицы: $A=\left$ и $B=\left$. И определим для них операцию умножения.

По-моему, тут всё очевидно. Дальше можно не читать.

У тех, кто впервые видит это определение, сразу возникает два вопроса:

1. Что это за лютая дичь?
2. А почему так сложно?

Что ж, обо всём по порядку. Начнём с первого вопроса. Что означают все эти индексы? И как не ошибиться при работе с реальными матрицами?

Прежде всего заметим, что длинная строчка для расчёта ${{c}_{i;j}}$ (специально поставил точку с запятой между индексами, чтобы не запутаться, но вообще их ставить не надо — я сам задолбался набирать формулу в определении) на самом деле сводится к простому правилу:

1. Берём $i$-ю строку в первой матрице;
2. Берём $j$-й столбец во второй матрице;
3. Получаем две последовательности чисел. Перемножаем элементы этих последовательностей с одинаковыми номерами, а затем складываем полученные произведения.

Данный процесс легко понять по картинке:

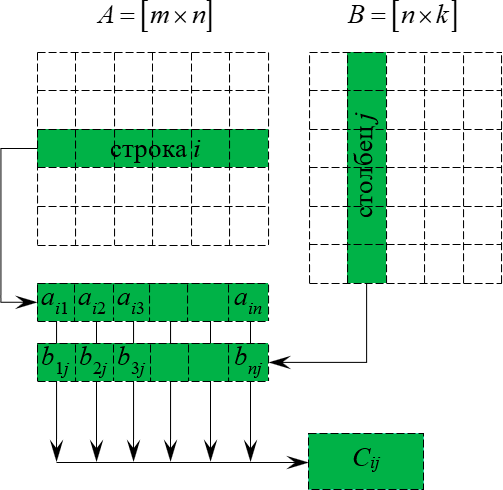Схема перемножения двух матриц

Ещё раз: фиксируем строку $i$ в первой матрице, столбец $j$ во второй матрице, перемножаем элементы с одинаковыми номерами, а затем полученные произведения складываем — получаем ${{c}_{ij}}$. И так для всех $1\le i\le m$ и $1\le j\le k$. Т.е. всего будет $m\times k$ таких «извращений».

Но хватит теории! Давайте посмотрим на реальные примеры. И начнём с самого простого случая — квадратных матриц.

Яндекс сколько стоит машина

Формулы массива в Excel

Под массивом обычно понимают набор данных, объединенных в группу. Массивы бывают одномерные (элементы массива образуют строку или столбец) или двумерные (матрица). Легко сообразить, что почти в любой таблице Excel при желании можно найти один или несколько таких массивов:

Формулы массива в Excel – это специальные формулы для обработки данных из таких массивов. Формулы массива делятся на две категории – те, что возвращают одно значение и те, что дают на выходе целый набор (массив) значений. Рассмотрим их на простых примерах…

Пример 1. Классика жанра – товарный чек

Задача: рассчитать общую сумму заказа. Если идти классическим путем, то нужно будет добавить столбец, где перемножить цену и количество, а потом взять сумму по этому столбцу. Если же применить формулу массива, то все будет гораздо красивее:

1. выделяем ячейку С7
2. вводим с клавиатуры =СУММ(
3. выделяем диапазон B2:B5
4. вводим знак умножения (звездочка)
5. выделяем диапазон C2:C5 и закрываем скобку функции СУММ – в итоге должно получиться так:
6. чтобы Excel воспринял нашу формулу как формулу массива жмем не Enter, как обычно, а Ctrl + Shift + Enter

Вуаля!

Т.е. Excel произвел попарное умножение элементов массивов B2:B5 и C2:C5 и образовал новый массив стоимостей (в памяти компьютера), а затем сложил все элементы этого нового массива.

Обратите внимание на фигурные скобки, появившиеся в формуле – отличительный признак формулы массива. Вводить их вручную с клавиатуры бесполезно – они автоматически появляются при нажатии Ctrl + Shift + Enter

Пример 2. Разрешите Вас… транспонировать?

При работе с таблицами часто возникает необходимость поменять местами строки и столбцы, т.е. развернуть таблицу на бок, чтобы данные, которые раньше шли по строке, теперь располагались в столбцах и наоборот. В математике такая операция называется транспонированием. При помощи формулы массива и функции ТРАНСП (TRANSPOSE) это делается на раз.

Допустим, имеем двумерный массив ячеек, который хотим транспонировать.

• Выделяем диапазон ячеек для размещения транспонированной таблицы. Поскольку исходный массив ячеек был 8 строк на 2 столбца, то надо выделить диапазон пустых ячеек размером 2 строки на 8 столбцов.
• вводим функцию транспонирования =ТРАНСП(   
• в качестве аргумента функции выделяем наш массив ячеек A1:B8

жмем Ctrl + Shift + Enter и получаем “перевернутый массив” в качестве результата:

Редактирование формулы массива

Если формула массива расположена не в одной ячейке (как в Примере 1), а в нескольких ячейках (как в Примере 2), то Excel не позволит редактировать или удалить одну отдельно взятую формулу (например в ячейке D10) и выдаст предупреждающее сообщение Невозможно изменить часть массива.

Для редактирования формулы массива необходимо выделить весь диапазон (A10:H11 в нашем случае) и изменить формулу в строке формул (или нажав F2). Затем необходимо повторить ввод измененной формулы массива, нажав сочетание клавиш Ctrl + Shift + Enter.

Excel также не позволит свободно перемещать ячейки, входящие в формулу массива или добавлять новые строки-столбцы-ячейки в диапазон формулы массива (т.е. в диапазон A10:H11 в нашем случае)

Пример 3. Таблица умножения

Вспомните детство, школу, свою тетрадку по математике… На обороте тетради на обложке было что? Таблица умножения вот такого вида:

При помощи формул массива она вся делается в одно движение:

1. выделяем диапазон B2:K11
2. вводим формулу =A2:A11*B1:K1
3. жмем Ctrl + Shift + Enter, чтобы Excel воспринял ее как формулу массива

и получаем результат:

Пример 4. Выборочное суммирование

Посмотрите как при помощи одной формулы массива красиво и легко выбираются данные по определенному товару и заказчику:

 В данном случае формула массива синхронно пробегает по всем элементам диапазонов C3:C21 и B3:B21, проверяя, совпадают ли они с заданными значениями из ячеек G4 и G5. Если совпадения нет, то результат равенства ноль, если совпадение есть, то единица. Таким образом суммы всех сделок, где заказчик не ANTON и товар не Boston Crab Meat умножаются на ноль и суммируются только нужные заказы.

2.7. Регрессия

Для построения используются
несколько стандартных функций листа.

TREND / ТЕНДЕНЦИЯ

Строит

y=b+m₁x₁+…+m_J x_J+e

Аппроксимирует известные значения вектора откликов
known_y’s для заданных значений матрицы предикторов
known_x’s и возвращает значения y,
для заданного массива new_x’s.  

Синтаксис 

TREND(known_y’s
)

Примечания 

• Вектор
  known_y’s должен занимать один столбец,
  тогда каждый столбец матрицы массива known_x’s
  интерпретируется как отдельная переменная;

• Если
  аргумент known_x’sопущен, то предполагается, что это вектор чисел {1;2;3;…}
  такого же размера, как и known_y’s;

• Матрица
  новых значений new_x’sдолжна иметь столько же столбцов
  (переменных), как и матрица known_x’s;

• Если
  аргумент new_x’sопущен, то предполагается, что он совпадает с
  массивом known_x’s.
  Результат является вектором, в котором число строк равно
  числу строк в массиве new_x’s.

Пример 
 

Рис.34 Функция TREND

Функция TRENDявляется функцией
массива и ее ввод должен завершаться нажатием комбинации
CTRL+SHIFT+ENTER. 

LINEST /
ЛИНЕЙН

Дополняет функцию TREND и выводит некоторые
статистические значения, связанные с регрессией  

y=b+m₁x₁+…+m_J x_J+e

Синтаксис 

LINEST(known_y’s
)

Рис. 35 Таблица вывода функция LINEST

m_J, …,
m₂, m₁
и b – оценки регрессионных
коэффициентов;

s_J, …,
s₂, s₁
и s_b
– стандартные ошибки для оценок регрессионных коэффициентов;

R2 –
коэффициент детерминации;

s_y –
стандартная ошибка оценки y;

F – F-статистика;

DoF – число степеней
свободы;

SS_reg –
регрессионная сумма квадратов;

SS_res–
остаточная сумма квадратов.

Примечания 

• LINEST – это
  очень плохо сконструированная функция, очень неудобная в
  практическом применении;

• Примечания,
  представленные в описании функции полностью применимы к
  функции LINEST.

Пример 
 

Рис.36 Функция LINEST

Функция LINEST является функцией массива и ее ввод должен
завершаться нажатием комбинации CTRL+SHIFT+ENTER. 

Как решить систему уравнений матричным методом в Excel

Дана система уравнений:

1. Значения элементов введем в ячейки Excel в виде таблицы.
2. Найдем обратную матрицу. Выделим диапазон, куда впоследствии будут помещены элементы матрицы (ориентируемся на количество строк и столбцов в исходной матрице). Открываем список функций (fx). В категории «Математические» находим МОБР. Аргумент – массив ячеек с элементами исходной матрицы.
3. Нажимаем ОК – в левом верхнем углу диапазона появляется значение. Последовательно жмем кнопку F2 и сочетание клавиш Ctrl + Shift + Enter.
4. Умножим обратную матрицу Ах-1х на матрицу В (именно в таком порядке следования множителей!). Выделяем диапазон, где впоследствии появятся элементы результирующей матрицы (ориентируемся на число строк и столбцов матрицы В). Открываем диалоговое окно математической функции МУМНОЖ. Первый диапазон – обратная матрица. Второй – матрица В.
5. Закрываем окно с аргументами функции нажатием кнопки ОК. Последовательно нажимаем кнопку F2 и комбинацию Ctrl + Shift + Enter.

Получены корни уравнений.

Выполнение расчетов

Вычисление обратной матрицы в Excel возможно только в том случае, если первичная матрица является квадратной, то есть количество строк и столбцов в ней совпадает. Кроме того, её определитель не должен быть равен нулю. Для вычисления применяется функция массива МОБР. Давайте на простейшем примере рассмотрим подобное вычисление.

Расчет определителя

Прежде всего, вычислим определитель, чтобы понять, имеет первичный диапазон обратную матрицу или нет. Это значение рассчитывается при помощи функции МОПРЕД.

1. Выделяем любую пустую ячейку на листе, куда будут выводиться результаты вычислений. Жмем на кнопку «Вставить функцию», размещенную около строки формул.
2. Запускается Мастер функций. В перечне записей, который он представляет, ищем «МОПРЕД», выделяем этот элемент и жмем на кнопку «OK».
3. Открывается окно аргументов. Ставим курсор в поле «Массив». Выделяем весь диапазон ячеек, в котором расположена матрица. После того, как его адрес появился в поле, жмем на кнопку «OK».
4. Программа производит расчет определителя. Как видим, для нашего конкретного случая он равен – 59, то есть не тождественен нулю. Это позволяет сказать, что у данной матрицы существует обратная.

Расчет обратной матрицы

Теперь можно преступить к непосредственному расчету обратной матрицы.

1. Выделяем ячейку, которая должна стать верхней левой ячейкой обратной матрицы. Переходим в Мастер функций, кликнув по значку слева от строки формул.
2. В открывшемся списке выбираем функцию МОБР. Жмем на кнопку «OK».
3. В поле «Массив», открывшегося окна аргументов функции, устанавливаем курсор. Выделяем весь первичный диапазон. После появления его адреса в поле, жмем на кнопку «OK».
4. Как видим, появилось значение только в одной ячейке, в которой была формула. Но нам нужна полноценная обратная функция, поэтому следует скопировать формулу в другие ячейки. Выделяем диапазон, равнозначный по горизонтали и вертикали исходному массиву данных. Жмем на функциональную клавишу F2, а затем набираем комбинацию Ctrl+Shift+Enter. Именно последняя комбинация предназначена для обработки массивов.
5. Как видим, после этих действий обратная матрица вычислена в выделенных ячейках.

На этом расчет можно считать завершенным.

Если вы производите расчет определителя и обратной матрицы только при помощи ручки и бумаги, то над этим вычислением, в случае работы над сложным примером, можно ломать голову очень долго. Но, как видим, в программе Эксель данные вычисления производятся очень быстро, независимо от сложности поставленной задачи. Для человека, который знаком с алгоритмом подобных расчетов в этом приложении, все вычисление сводится к чисто механическим действиям.

Мы рады, что смогли помочь Вам в решении проблемы.

Помогла ли вам эта статья?

Нахождение обратной матрицы всегда вызывало большие затруднения у учащихся, так как это был очень трудоемкий процесс. И вот такое задание вполне по силам EXCEL.  

Прежде всего, уясним одно правило:  Матрица имеет обратную только тогда, когда ее определитель не равен нулю.  А вот и задание: найдите матрицу, обратную к матрице А, где

Вычислять определитель этой матрицы мы умеем. Я его уже вычислил.

Он оказался равен -4, а  это значит, что у нашей матрицы есть обратная (если бы определитель оказался равен нулю, то мы сказали бы что матрица не имеет обратную и немедленно прекратили все вычисления). Теперь отметим ячейку, с которой начнем записывать ответ. Я отметил ячейку E1.  Нажимаем Формулы, затем Математические и в появившемся окне находим  МОБР

После нажатия появляется вот такое окно, в котором надо вписать адреса ячеек, в которых находятся элементы матрицы  в Массив

У нас элементы записаны в ячейки начиная с А1 и заканчивая в С3 , поэтому так и записываем (смотрите картинку)

Если все сделали правильно, то автоматически заполнится место, обведенное красным и запишется ответ, который обведен черным. В таком виде ответ трудно переваривать и поэтому нажимаем ОК.  В ячейке, которую мы застолбили под ответ, появилось число 3,  Это только первый элемент полученной обратной матрицы.

Чтобы виден был весь ответ, выполняем следующие действия: Начиная с  ячейки Е1 выделяем три строчки и три столбца (именно столько было у исходной матрицы и столько же будет у обратной)

нажимаем клавишу F2,  а затем на одновременно на три клавиши  Ctrl+Shift+Enter.

В выделенном месте появляются, теперь уже все, элементы обратной матрицы. Если Вы сохраните этот документ, то в следующий раз можете воспользоваться плодами своего труда. Так, меняя элементы исходной матрицы, Вы автоматически получаете для нее же обратную матрицу.

На этом все. Крепких вам знаний.

Рубрика: EXCEL в помощь, Статьи. Метки: EXCEL, ИКТ, матрица, обратная матрица

2.9. Виртуальный массив

При анализе данных часто возникает проблема сохранения
промежуточных результатов, которые нужны не сами по себе, а только для
того, чтобы вычислить по ним другие, полезные значения. Например,
остатки в методе PCA часто нам не интересны, а нужны только для
определения полной объясненной дисперсии, ортогональных расстояний и
т.п. При этом размеры таких промежуточных массивов могут быть очень
велики, да и к тому же их приходится вычислять при различных значениях
числа главных компонент. Все это ведет к заполнению рабочей книги
большим количеством ненужных, промежуточных результатов. Этого можно
избежать, если использовать виртуальные массивы. Поясним их суть на
простом примере. 

Рис.38 Пример использования виртуального
массива

Предположим, что задана матрица A, а
нужно вычислить детерминант матрицы AtA
. На Рис. 38 показаны два способа вычисления. Первый – через
последовательность промежуточных массивов, отмеченных красными
стрелками. Второй – с помощью одной формулы, показанной зеленой
стрелкой. Оба пути ведут к одному и тому же результату, но красный путь
занимает на листе много места, а зеленый последовательно использует
несколько промежуточных виртуальных массивов. Все они, по сути,
совпадают с реальными массивами красного пути, но на лист не выводятся.

Первый массив –  это транспонированная матрица At,
получаемая как результат функции
(A).

Второй виртуальный массив получается тогда, когда первый
виртуальный массив умножается на матрицу A с помощью
функции (TRANSPOSE(A), A).  

И, наконец, к этому, второму виртуальному массиву применяется функция
.

Виртуальные массивы очень полезны при вычислении всяческих
вспомогательных характеристик в анализе многомерных данных: остатков,
собственных значений, и т.п. Подробно об этом рассказывается в пособии
Расширение возможностей Chemometrics Add-In.

Решение матриц в Excel

С матрицами в Excel выполняются такие операции, как: транспонирование, сложение, умножение на число / матрицу; нахождение обратной матрицы и ее определителя.

Транспонирование

Транспонировать матрицу – поменять строки и столбцы местами.

Сначала отметим пустой диапазон, куда будем транспонировать матрицу. В исходной матрице 4 строки – в диапазоне для транспонирования должно быть 4 столбца. 5 колонок – это пять строк в пустой области.

• 1 способ. Выделить исходную матрицу. Нажать «копировать». Выделить пустой диапазон. «Развернуть» клавишу «Вставить». Открыть меню «Специальной вставки». Отметить операцию «Транспонировать». Закрыть диалоговое окно нажатием кнопки ОК.
• 2 способ. Выделить ячейку в левом верхнем углу пустого диапазона. Вызвать «Мастер функций». Функция ТРАНСП. Аргумент – диапазон с исходной матрицей.

Нажимаем ОК. Пока функция выдает ошибку. Выделяем весь диапазон, куда нужно транспонировать матрицу. Нажимаем кнопку F2 (переходим в режим редактирования формулы). Нажимаем сочетание клавиш Ctrl + Shift + Enter.

Преимущество второго способа: при внесении изменений в исходную матрицу автоматически меняется транспонированная матрица.

Сложение

Складывать можно матрицы с одинаковым количеством элементов. Число строк и столбцов первого диапазона должно равняться числу строк и столбцов второго диапазона.

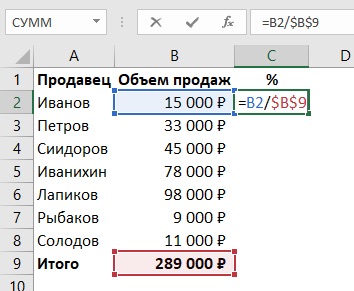
В первой ячейке результирующей матрицы нужно ввести формулу вида: = первый элемент первой матрицы + первый элемент второй: (=B2+H2). Нажать Enter и растянуть формулу на весь диапазон.

Умножение матриц в Excel

Чтобы умножить матрицу на число, нужно каждый ее элемент умножить на это число. Формула в Excel: =A1*$E$3 (ссылка на ячейку с числом должна быть абсолютной).

Умножим матрицу на матрицу разных диапазонов. Найти произведение матриц можно только в том случае, если число столбцов первой матрицы равняется числу строк второй.

В результирующей матрице количество строк равняется числу строк первой матрицы, а количество колонок – числу столбцов второй.

Для удобства выделяем диапазон, куда будут помещены результаты умножения. Делаем активной первую ячейку результирующего поля. Вводим формулу: =МУМНОЖ(A9:C13;E9:H11). Вводим как формулу массива.

Обратная матрица в Excel

Ее имеет смысл находить, если мы имеем дело с квадратной матрицей (количество строк и столбцов одинаковое).

Размерность обратной матрицы соответствует размеру исходной. Функция Excel – МОБР.

Выделяем первую ячейку пока пустого диапазона для обратной матрицы. Вводим формулу «=МОБР(A1:D4)» как функцию массива. Единственный аргумент – диапазон с исходной матрицей. Мы получили обратную матрицу в Excel:

Печь на отработанном масле: варианты изготовления устройства своими руками

Учимся программировать

Задание 1. Транспонировать данную матрицу

1. Заполните ячейки таблицы значениями элементов матрицы (рис.1).

Рисунок 1.

Выделите диапазон ячеек (рис.2) – здесь будет располагаться транспонированная матрица.

Рисунок 2.

Вызовите мастер функций (меню Вставка-Функция или значок Вставить функцию в строке формул). В категории «Полный алфавитный перечень» найдите функцию «ТРАНСП» и нажмите ОК.

Рисунок 3.

В появившемся окне введите диапазон значений исходной матрицы.

Рисунок 4.

Для получения результата одновременно нажмите клавиши «Ctrl»+«Shift»+«Enter».

Рисунок 5.

2. Умножение матрицы на числоЗадание 2. Дана матрица А (рис.6). Получить матрицу B=3*А. Ход работы:

1. Введите матрицу (рис.6).
2. Выделите ячейку E1 и введите формулу =3*A1.
3. Скопируйте введенную формулу в остальные ячейки результирующей матрицы: для этого наведите курсор на точку в правом нижнем углу ячейки, так, чтобы курсор изменился на тонкий крестик, нажмите на левую кнопку мыши и протяните до ячейки G1. Таким же образом протяните указатель до ячейки G2.
4. В результате должна получиться матрица B (рис.7):

Рисунок 6. Матрица A

Рисунок 7. Матрица B

3. Сложение матрицЗадание 3. Сложить две матрицы A и B (даны на рис.8).

Рисунок 8.

Ход работы:

1. Введите две матрицы A и B (рис.8).
2. Выделите первую ячейку результирующей матрицы D5 и внесите формулу =B1+F1.
3. Скопируйте формулу на оставшиеся ячейки матрицы C.

Рисунок 9. Результат

Уровень 2

4.Умножение матрицЗадание 4.Даны матрицы А и В (рис.10). Найти их произведение С=А*В.

Рисунок 10.

Ход работы:

1. Выделяем мышкой при нажатой левой кнопке соответствующий диапазон ячеек D5:E7 (строк такое же количество как в матрице А, а столбцов такое же количество как в матрице В).
2. Вызываем мастер функций и в категории «Полный алфавитный перечень находим функцию «МУМНОЖ» и нажимаем ОК.

1. В появившемся окне вводим диапазон значений исходных матриц А и В (рис.11).

Рисунок 11.

1. Для получения результата нажимаем сочетание клавиш «Shift»+«Ctrl»+«Enter».

Рисунок 12

Задание 5. Самостоятельно с помощью функции ТРАНС транспонировать следующую матрицу.

Рисунок 13.

Уровень 3

Задание 6. Самостоятельно выполнить с помощью Excel умножение матриц А и В. Даны А и В. В результате вычислений должна получиться матрица C (рис.14)

Рисунок 14.

Задание 7.  Даны матрицы А, В, С и число a=2. Найти

Подсказка: Все вычисления выполнять на одном листе. Сначала вычислить, затем умножить матрицы , далее умножить матрицу С на число a, затем сложить  матрицы  и aС.Тест: результат Задание 8. Даны матрицы А, В, С и число a=2. Найти

Тест: результат

Вопросы на повторение:

1. Какая функция в Excel используется для транспонирования матрицы?
2. Какая функция в Excel используется для умножения матриц?

Уровень 1

Задание 1: найти произведение матриц AB, где

Задание 2: найти произведение матриц BA, где

Задание 3:  Даны матрицы А, В. Найти

Тест:

Знакомство со сложными формулами в Excel — Microsoft Excel для начинающих

В этом уроке мы познакомимся с понятием Сложная формула в Excel, а также разберем порядок выполнения действий при решении таких формул. Представленная информация является базовой и предназначена в первую очередь для начинающих пользователей Microsoft Excel.

Простая формула – это математическое выражение с одним оператором, такое как 7+9. Сложная формула содержит более одного оператора, к примеру, 5+2*8.

Используя Excel для вычисления сложных формул, необходимо знать порядок выполнения действий.

Порядок действий в формулах Excel

Excel выполняет действия, опираясь на следующий порядок:

1. Выражения, помещенные в скобки.
2. Возведение в степень (например, 3^2).
3. Умножение и деление, что идет раньше.
4. Сложение и вычитание, что идет раньше.

Пример решения сложной формулы

В качестве примера, попробуем вычислить значение формулы, представленной на следующем рисунке. На первый взгляд это выражение выглядит довольно сложным, но мы можем воспользоваться порядком выполнения операций поэтапно, чтобы найти правильный ответ.

В первую очередь, мы начнем с выполнения действия в скобках. В данном случае нам необходимо вычислить: 6-3=3.

Возведение в степень

Можно заметить, что сложная формула теперь выглядит немного проще. Далее мы проверим наличие степеней в нашем выражении. Да, она встречается один раз: 2^2=4.

Деление

Далее мы выполним все операции умножения и деления, в порядке следования слева направо. Поскольку деление встречается раньше умножения, то деление выполняется первым: 3/4=0,75.

Теперь мы выполним оставшуюся операцию умножения: 0,75*4=3.

Сложение

Далее мы выполним все операции сложения и вычитания, в порядке следования слева направо. Поскольку сложение встречается раньше вычитания, то сложение выполняется первым: 10+3=13.

Вычитание

В заключение остается последнее действие – вычитание: 13-1=12.

В итоге мы получили ответ: 12.

Точно такой же результат вы получите, если введете эту формулу в Excel.

Как видите, в этом нет ничего сложного!

Оцените качество статьи

Нам важно ваше мнение: