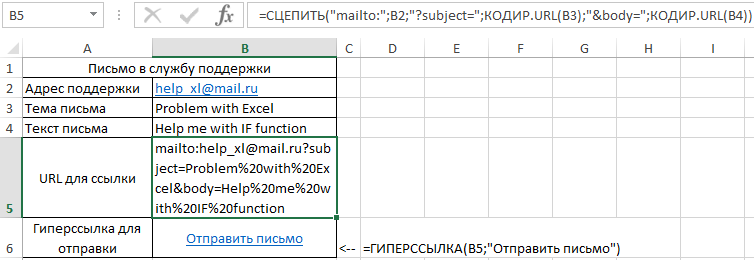
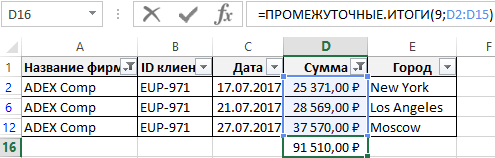
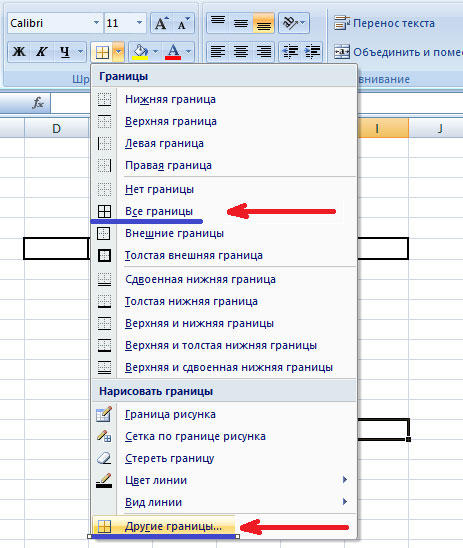
Как сделать проверку обратной матрицы в excel?

Нахождение обратной матрицы с помощью элементарных преобразований (метод Гаусса)

Пример 3. Методом элементарных преобразований вычислить -1 если = .

Решение. Приписываем к исходной справа единичную того же порядка: . С помощью элементарных преобразований столбцов приведём левую “половину” к единичной, совершая одновременно точно такие преобразования над правой «половиной».
Поменяем местами 1 со 2 столбцы: ~. К третьему прибавим первый, ко второму — первый, × на -2: . Из первого вычтем удвоенный второй, из третьего — × на 6 второй; . Прибавим третий к первому и второму: . Умножим последний на минус один: . Справа от вертикальной черты квадратная таблица размером 3х3 .

Сложение и вычитание матриц в Excel

Способ 1

Следует отметить, что складывать и вычитать можно матрицы одинаковой размерности (одинаковое количество строк и столбцов у каждой из матриц). Причем каждый элемент результирующей матрицы С будет равен сумме соответствующих элементов матриц А и В, т.е. с_ij = а_ij + b_ij.

Рассмотрим матрицы А и В размерностью 3х4. Вычислим сумму этих матриц. Для этого в ячейку N3 введем формулу =B3+H3, где B3 и H3 – первые элементы матриц А и В соответственно. При этом формула содержит относительные ссылки (В3 и H3), чтобы при копировании формулы на весь диапазон матрицы С они могли измениться.

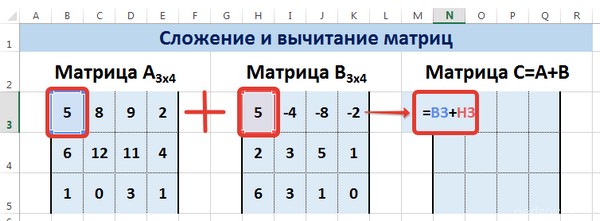
С помощью маркера автозаполнения скопируем формулу из ячейки N3 вниз и вправо на весь диапазон матрицы С.

Для вычитания матрицы В из матрицы А (С=А — В) в ячейку N3 введем формулу =B3 — H3 и скопируем её на весь диапазон матрицы С.

Способ 2

Этот способ отличается тем, что результат сложения/вычитания матриц сам является массивом. В этом случае нельзя удалить элемент массива.

Для деления матрицы на число этим способом выделяем диапазон, в котором будет вычислен результат, вводим знак «=», выделяем диапазон, содержащий первую матрицу А, нажимаем на клавиатуре знак сложения (+) и выделяем вторую матрицу В. После ввода формулы нажимаем сочетание клавиш Ctrl+Shift+Enter, чтобы значениями заполнился весь диапазон.

1.2. Книга, лист и ячейка

Файл Excel с расширением XLS (XLSX в версии 2007) называется
(рабочей) книгой. Если запустить программу Excel, например, щелкнуть на
рабочем столе иконку
,
то откроется новая пустая книга. . 

Рис. 2 Новая книга Excel

Если рабочая книга уже существует, то ее проще открыть через проводник. Для
этого достаточно щелкнуть по иконке файла.  

Рис. 3
Открытие книги Excel через проводник

Рабочая книга состоит из нескольких листов, имена которых
показаны в нижней части окна. Листы можно удалять, добавлять,
переименовывать. Для этого надо щелкнуть правой клавишей мышки по имени
листа. Появится меню, из которого можно выбрать нужную операцию.

Рис.
4 Операции с листами

Стандартное имя листа – Sheet1, но ему можно дать любое имя, например
Data. На лист можно вставлять рисунки, графики и другие необходимые
объекты.

Каждый лист состоит из ячеек, образующих таблицу, размером 256
столбцов и 65536 строк (В версии 2007 – 16384 столбцов и1048576 строк).
Строки на листе обозначены числами: 1,2, 3…, а столбцы имеют буквенную
кодировку: A, B, …,Z,
AA, AB .., и т.д. до последнего столбца
IV (в 2007
– до XFD). Этот стиль адресации называется A1. Реже применяется
альтернативный стиль R1C1, в котором столбцы также нумеруются. Мы не
будем использовать этот стиль, а прочитать об этом можно

здесь

Строки и столбцы можно удалять, добавлять, прятать, а также менять их размер:
высоту или ширину.

Все операции на листе выполняются с помощью меню, представленного в
верхней части окна (). Меню в Excel 2007
существенно отличается от прежней версии. Там, вместо обычных иконок,
появилась лента. Мы не будем подробно разбирать отличия версий. Те, кому
это интересно могут прочитать

здесь.

Нахождение обратной матрицы методом алгебраических дополнений (союзной матрицы)

Для неособенной квадратной матрицы А обратной является матрица

,  (2)

где —
определитель матрицы А, а

— матрица, союзная с матрицей А.

Разберём ключевые понятия, которые потребуются для решения задач — союзная матрица, алгебраические дополнения и транспонированная матрица.

Пусть существует квадратная матрица A:

Транспонированная относительно матрицы A матрица A’ получается,
если из строк матрицы A сделать столбцы, а из её столбцов — наоборот, строки, то есть заменить строки
столбцами:

Остановимся на минорах и алгебраических дополнениях.

Пусть есть квадратная матрица третьего порядка:

.

Её определитель:

Вычислим алгебраическое дополнение элемента ,
то есть элемента 2, стоящего на пересечении первой строки и второго столбца.

Для этого нужно сначала найти минор этого элемента. Он получается вычёркиванием из
определителя строки и столбца, на пересечении которых стоит указанный элемент. В результате останется
следующий определитель, который и является минором элемента :

.

Алгебраическое дополнение элемента
получим, если умножим ,
где i — номер строки исходного элемента, а k — номер столбца исходного элемента, на
полученный в предыдущем действии минор этого исходного элемента. Получаем алгебраическое дополнение элемента
:

.

По этой инструкции нужно вычислить алгебраические дополнения всех элементов матрицы
A’, транспонированной относительно матрицы матрица A.

И последнее из значимых для нахождение обратной матрицы понятий. Союзной с квадратной матрицей A называется матрица

того же порядка, элементами которой являются алгебраические дополнения соответствующих элементов определителя матрицы
,
транспонированной относительно матрицы A. Таким образом, союзная матрица состоит из следующих элементов:

Алгоритм нахождения обратной матрицы методом алгебраических дополнений

1. Найти определитель данной матрицы A. Если определитель равен нулю, нахождение
обратной матрицы прекращается, так как матрица вырожденная и обратная для неё не существует.

2. Найти матрицу, транспонированную относительно A.

3. Вычислить элементы союзной матрицы как алгебраические дополнения марицы, найденной на шаге 2.

4. Применить формулу (2): умножить число, обратное определителю матрицы A,
на союзную матрицу, найденную на шаге 4.

5. Проверить полученный на шаге 4 результат, умножив данную матрицу A на
обратную матрицу. Если произведение этих матриц равно единичной матрицы, значит обратная матрица была
найдена верно. В противном случае начать процесс решения снова.

Пример 1. Для матрицы

найти обратную матрицу.

Решение. Для нахождения обратной матрицы необходимо найти определитель матрицы А .
Находим по правилу треугольников:

Следовательно, матрица А – неособенная (невырожденная, несингулярная) и для неё существует обратная.

Найдём матрицу, союзную с данной матрицей А.

Найдём матрицу
,
транспонированную относительно матрицы A:

Вычисляем элементы союзной матрицы как алгебраические дополнения матрицы,
транспонированной относительно матрицы A:

Следовательно, матрица
,
союзная с матрицей A, имеет вид

Замечание. Порядок вычисления элементов и транспонирования матрицы может
быть иным. Можно сначала вычислить алгебраические дополнения матрицы A, а затем транспонировать
матрицу алгебраических дополнений. В результате должны получиться те же элементы союзной матрицы.

Применяя формулу (2), находим матрицу, обратную матрице А:

Проверить решение можно с помощью онлайн калькулятора
для нахождения обратной матрицы.

Как найти валовый показатель по матрице взаимосвязей?

Пример 2. Связь между тремя отраслями представлена матрицей прямых затрат А. Спрос (конечный продукт) задан вектором X. Найти валовой выпуск продукции отраслей Х. Описать используемые формулы, представить распечатку со значениями и с формулами.

Исходные данные приведены на рисунке 2:

Рисунок 2 – Исходные данные.

Данная задача связана с определением объема производства каждой из N отраслей, чтобы удовлетворить все потребности в продукции данной отрасли. При этом каждая отрасль выступает и как производитель некоторой продукции и как потребитель своей и произведенной другими отраслями продукции. Задача межотраслевого баланса – отыскание такого вектора валового выпуска X, который при известной матрице прямых затрат обеспечивает заданный вектор конечного продукта Y.

Матричное решение данной задачи:

где Е – единична матрица.

Для решения задачи в примере используем следующие 4 функции для работы с матрицами в Excel:

1. МОБР – нахождение обратной матрицы.
2. МУМНОЖ – умножение матриц.
3. МОПРЕД – нахождение определителя матрицы.
4. МЕДИН – нахождение единичной матрицы.

Результаты приведены на рисунке 3:

Рисунок 3 – Результат вычислений.

Выполнение расчетов

Вычисление обратной матрицы в Excel возможно только в том случае, если первичная матрица является квадратной, то есть количество строк и столбцов в ней совпадает. Кроме того, её определитель не должен быть равен нулю. Для вычисления применяется функция массива МОБР. Давайте на простейшем примере рассмотрим подобное вычисление.

Расчет определителя

Прежде всего, вычислим определитель, чтобы понять, имеет первичный диапазон обратную матрицу или нет. Это значение рассчитывается при помощи функции МОПРЕД.

1. Выделяем любую пустую ячейку на листе, куда будут выводиться результаты вычислений. Жмем на кнопку «Вставить функцию», размещенную около строки формул.
2. Запускается Мастер функций. В перечне записей, который он представляет, ищем «МОПРЕД», выделяем этот элемент и жмем на кнопку «OK».
3. Открывается окно аргументов. Ставим курсор в поле «Массив». Выделяем весь диапазон ячеек, в котором расположена матрица. После того, как его адрес появился в поле, жмем на кнопку «OK».
4. Программа производит расчет определителя. Как видим, для нашего конкретного случая он равен – 59, то есть не тождественен нулю. Это позволяет сказать, что у данной матрицы существует обратная.

Расчет обратной матрицы

Теперь можно преступить к непосредственному расчету обратной матрицы.

1. Выделяем ячейку, которая должна стать верхней левой ячейкой обратной матрицы. Переходим в Мастер функций, кликнув по значку слева от строки формул.
2. В открывшемся списке выбираем функцию МОБР. Жмем на кнопку «OK».
3. В поле «Массив», открывшегося окна аргументов функции, устанавливаем курсор. Выделяем весь первичный диапазон. После появления его адреса в поле, жмем на кнопку «OK».
4. Как видим, появилось значение только в одной ячейке, в которой была формула. Но нам нужна полноценная обратная функция, поэтому следует скопировать формулу в другие ячейки. Выделяем диапазон, равнозначный по горизонтали и вертикали исходному массиву данных. Жмем на функциональную клавишу F2, а затем набираем комбинацию Ctrl+Shift+Enter. Именно последняя комбинация предназначена для обработки массивов.
5. Как видим, после этих действий обратная матрица вычислена в выделенных ячейках.

На этом расчет можно считать завершенным.

Если вы производите расчет определителя и обратной матрицы только при помощи ручки и бумаги, то над этим вычислением, в случае работы над сложным примером, можно ломать голову очень долго. Но, как видим, в программе Эксель данные вычисления производятся очень быстро, независимо от сложности поставленной задачи. Для человека, который знаком с алгоритмом подобных расчетов в этом приложении, все вычисление сводится к чисто механическим действиям.

Мы рады, что смогли помочь Вам в решении проблемы.

Помогла ли вам эта статья?

Нахождение обратной матрицы всегда вызывало большие затруднения у учащихся, так как это был очень трудоемкий процесс. И вот такое задание вполне по силам EXCEL.  

Прежде всего, уясним одно правило:  Матрица имеет обратную только тогда, когда ее определитель не равен нулю.  А вот и задание: найдите матрицу, обратную к матрице А, где

Вычислять определитель этой матрицы мы умеем. Я его уже вычислил.

Он оказался равен -4, а  это значит, что у нашей матрицы есть обратная (если бы определитель оказался равен нулю, то мы сказали бы что матрица не имеет обратную и немедленно прекратили все вычисления). Теперь отметим ячейку, с которой начнем записывать ответ. Я отметил ячейку E1.  Нажимаем Формулы, затем Математические и в появившемся окне находим  МОБР

После нажатия появляется вот такое окно, в котором надо вписать адреса ячеек, в которых находятся элементы матрицы  в Массив

У нас элементы записаны в ячейки начиная с А1 и заканчивая в С3 , поэтому так и записываем (смотрите картинку)

Если все сделали правильно, то автоматически заполнится место, обведенное красным и запишется ответ, который обведен черным. В таком виде ответ трудно переваривать и поэтому нажимаем ОК.  В ячейке, которую мы застолбили под ответ, появилось число 3,  Это только первый элемент полученной обратной матрицы.

Чтобы виден был весь ответ, выполняем следующие действия: Начиная с  ячейки Е1 выделяем три строчки и три столбца (именно столько было у исходной матрицы и столько же будет у обратной)

нажимаем клавишу F2,  а затем на одновременно на три клавиши  Ctrl+Shift+Enter.

В выделенном месте появляются, теперь уже все, элементы обратной матрицы. Если Вы сохраните этот документ, то в следующий раз можете воспользоваться плодами своего труда. Так, меняя элементы исходной матрицы, Вы автоматически получаете для нее же обратную матрицу.

На этом все. Крепких вам знаний.

Рубрика: EXCEL в помощь, Статьи. Метки: EXCEL, ИКТ, матрица, обратная матрица

1.3. Адресация

A1C5Name BoxA1F=адрес=A1

Например, первая ячейка имеет абсолютный адрес –  $A$1, относительный адрес –
A1, и два
смешанных адреса – $A1 и
A$1. Различие в способе адресации проявляется,
прежде всего, тогда, когда формула копируется и переносится в другое
место. Поясним это на простом примере.

Рис. 5 Абсолютная и относительная адресация

На верхней панели показан фрагмент листа с
данными, выделенными желтым цветом. В зеленых областях (столбец
F и строка 6)
приведены различные варианты адресации одной и той же ячейки –
A1 (выделена оранжевым). Тип адресации
указан рядом с соответствующей ячейкой. Скопируем каждую из зеленых
областей (по очереди) и вставим рядом – в соседних столбцах:
G и H, и в
соседних строках: 7 и
8 (средняя панель ). Видно, что
результат зависит от типа адресации. Для абсолютной адресации ссылка на
первую ячейку сохранилась. Для относительной – ссылка сдвигается вправо
или вниз, сохраняя относительное положение двух ячеек: той, где стоит
ссылка, и той, на которую ссылаются. Для смешанной адресации результат
зависит от того, куда переносится копия, и от того, какая часть адреса
фиксируется значком доллара $. На правой
панели показаны соответствующие формулы, получающиеся после копирования.
Заметим, что ссылки на ячейки могут изменяться в зависимости от способа
адресации, но при перемещении ячейки с формулой содержащиеся в формуле
ссылки не изменяются.

Для адресации ячейки, которая находится на другом листе той же книги,
надо указывать еще и имя листа, например: Data!B2.
Восклицательный знак (!) отделяет имя листа
от адреса ячейки. Если имя листа содержит пробел, тогда имя надо
заключить в одинарные кавычки, например ‘Raw
Spectra’!C6. При адресации к другой книге, ее имя указывается
впереди, в квадратных скобках, например;
Results!P24

Подробнее о способах адресации можно прочитать

здесь.

2.9. Виртуальный массив

При анализе данных часто возникает проблема сохранения
промежуточных результатов, которые нужны не сами по себе, а только для
того, чтобы вычислить по ним другие, полезные значения. Например,
остатки в методе PCA часто нам не интересны, а нужны только для
определения полной объясненной дисперсии, ортогональных расстояний и
т.п. При этом размеры таких промежуточных массивов могут быть очень
велики, да и к тому же их приходится вычислять при различных значениях
числа главных компонент. Все это ведет к заполнению рабочей книги
большим количеством ненужных, промежуточных результатов. Этого можно
избежать, если использовать виртуальные массивы. Поясним их суть на
простом примере. 

Рис.38 Пример использования виртуального
массива

Предположим, что задана матрица A, а
нужно вычислить детерминант матрицы AtA
. На Рис. 38 показаны два способа вычисления. Первый – через
последовательность промежуточных массивов, отмеченных красными
стрелками. Второй – с помощью одной формулы, показанной зеленой
стрелкой. Оба пути ведут к одному и тому же результату, но красный путь
занимает на листе много места, а зеленый последовательно использует
несколько промежуточных виртуальных массивов. Все они, по сути,
совпадают с реальными массивами красного пути, но на лист не выводятся.

Первый массив –  это транспонированная матрица At,
получаемая как результат функции
(A).

Второй виртуальный массив получается тогда, когда первый
виртуальный массив умножается на матрицу A с помощью
функции (TRANSPOSE(A), A).  

И, наконец, к этому, второму виртуальному массиву применяется функция
.

Виртуальные массивы очень полезны при вычислении всяческих
вспомогательных характеристик в анализе многомерных данных: остатков,
собственных значений, и т.п. Подробно об этом рассказывается в пособии
Расширение возможностей Chemometrics Add-In.

Основные методы решения поставленной проблемы

Среди бесчисленного числа способов убрать большие буквы на компьютере, выделяют самые популярные и простые варианты решения.

Способ 1

Просто воспользуйтесь клавишами “контрл”(Ctrl) и “минус”(-). Данный метод является универсальным для большинства компьютерных программ ОС Windows, да и для стороннего программного обеспечения тоже. Просто нажмите на Ctrl и держите его, а затем жмите на минус — вы тут же увидите, как все уменьшается.

Способ 2

Также можно воспользоваться настройками браузера, который вы используете. Во время серфинга по пространству мировой сети может возникнуть потребность в уменьшении размеров шрифта, который этим браузером и отображается. Такие меры необходимы, для того чтобы серфинг был комфортным.

Чтобы “поиграться с буквами:

1. Просто зайдите в настройки программы и найдите там параметр, который отвечает за размеры.
2. Установите нужные значения и продолжайте пользоваться интернетом.
3. Если результат вас не удовлетворяет, то можете попробовать изменить масштаб страницы. В настройках будет меню, в котором обычно располагаются клавиши, отвечающие за регулировку размеров отображения в виде “минуса” и “плюса”.

Способ 3

Также вы можете попробовать управлять разрешением монитора. Разрешение — это количество точек, которые одновременно отображаются на экране. Если вы измените значения этого параметра, то и значки, и шрифты поменяют свой размер, будут выглядеть нагляднее, а эксплуатации персонального компьютера станет комфортнее.

Для того чтобы провернуть все эти действия, нажмите ПКМ (правой кнопкой мыши) по пустой области на пространстве рабочего стола и выберите раздел под названием “Разрешение экрана”, в котором необходимо переключиться на более высокие значения разрешения экрана.

Способ 4

Можно попробовать убавить величину букв при помощи встроенных стандартных средств операционной системы Windows. Данный способ также является эффективным, а для его применения понадобится только запущенный в рабочий режим компьютер:

1. Вам необходимо навести курсор компьютерной мыши на пустую область на рабочем пространстве и нажать ПКМ.
2. Перед вам раскроется контекстное меню, в котором необходимо выбрать раздел с названием “Персонализация”.
3. Теперь перейдите на вкладку “Цвет окна”, а после этого в “Дополнительные параметры оформления”. Там вы должны увидеть элементы, например “Значок” и проставьте те размеры, которые будут удовлетворять вашим потребностям. Здесь же вы сможете менять и визуализацию окон, и величину букв, которые системные окна используют.

Способ 5

Ну и напоследок можно воспользоваться настройкой экрана:

1. Перейдите в панель управления из меню “Пуск” и откройте “Управление и персонализация”.
2. Теперь ищем пункт “Экран”, заходим в него и настраиваем размер в меньшую сторону, если это возможно.

Операции с массивами

Массив – это группа данных, которая расположена на листе в смежных ячейках. По большому счету, любую таблицу можно считать массивом, но не каждый из них является таблицей, так как он может являться просто диапазоном. По своей сущности такие области могут быть одномерными или двумерными (матрицы). В первом случае все данные располагаются только в одном столбце или строке.

Во втором — в нескольких одновременно.

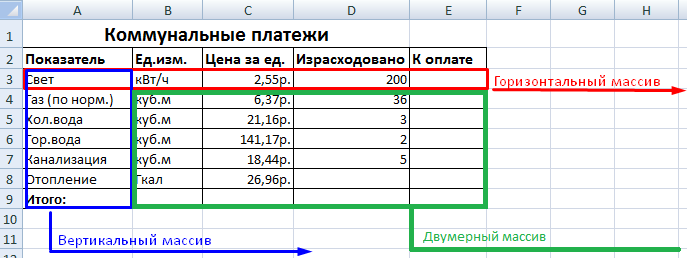
Кроме того, среди одномерных массивов выделяют горизонтальный и вертикальный тип, в зависимости от того, что они собой представляют – строку или столбец.

Нужно отметить, что алгоритм работы с подобными диапазонами несколько отличается от более привычных операций с одиночными ячейками, хотя и общего между ними тоже много. Давайте рассмотрим нюансы подобных операций.

Создание формулы

Формула массива – это выражение, с помощью которого производится обработка диапазона с целью получения итогового результата, отображаемого цельным массивом или в одной ячейке. Например, для того, чтобы умножить один диапазон на второй применяют формулу по следующему шаблону:

Над диапазонами данных можно также выполнять операции сложения, вычитания, деления и другие арифметические действия.

Координаты массива имеют вид адресов первой её ячейки и последней, разделенные двоеточием. Если диапазон двумерный, то первая и последняя ячейки расположены по диагонали друг от друга. Например, адрес одномерного массива может быть таким: A2:A7.

А пример адреса двумерного диапазона выглядит следующим образом: A2:D7.

1. Чтобы рассчитать подобную формулу, нужно выделить на листе область, в которую будет выводиться результат, и ввести в строку формул выражение для вычисления.

После ввода следует нажать не на кнопку Enter, как обычно, а набрать комбинацию клавиш Ctrl+Shift+Enter. После этого выражение в строке формул будет автоматически взято в фигурные скобки, а ячейки на листе будут заполнены данными, полученными в результате вычисления, в пределах всего выделенного диапазона.

Изменение содержимого массива

Если вы в дальнейшем попытаетесь удалить содержимое или изменить любую из ячеек, которая расположена в диапазоне, куда выводится результат, то ваше действие окончится неудачей. Также ничего не выйдет, если вы сделаете попытку отредактировать данные в строке функций. При этом появится информационное сообщение, в котором будет говориться, что нельзя изменять часть массива. Данное сообщение появится даже в том случае, если у вас не было цели производить какие-либо изменения, а вы просто случайно дважды щелкнули мышью по ячейке диапазона.

Если вы закроете, это сообщение, нажав на кнопку «OK», а потом попытаетесь переместить курсор с помощью мышки, или просто нажмете кнопку «Enter», то информационное сообщение появится опять. Не получится также закрыть окно программы или сохранить документ. Все время будет появляться это назойливое сообщение, которое блокирует любые действия. А выход из ситуации есть и он довольно прост

1. Закройте информационное окно, нажав на кнопку «OK».

Затем нажмете на кнопку «Отмена», которая расположена в группе значков слева от строки формул, и представляет собой пиктограмму в виде крестика. Также можно нажать на кнопку Esc на клавиатуре. После любой из этих операций произойдет отмена действия, и вы сможете работать с листом так, как и прежде.

Но что делать, если действительно нужно удалить или изменить формулу массива? В этом случае следует выполнить нижеуказанные действия.

Для изменения формулы выделите курсором, зажав левую кнопку мыши, весь диапазон на листе, куда выводится результат

Это очень важно, так как если вы выделите только одну ячейку массива, то ничего не получится. Затем в строке формул проведите необходимую корректировку

После того, как изменения внесены, набираем комбинацию Ctrl+Shift+Esc. Формула будет изменена.

1. Для удаления формулы массива нужно точно так же, как и в предыдущем случае, выделить курсором весь диапазон ячеек, в котором она находится. Затем нажать на кнопку Delete на клавиатуре.

После этого формула будет удалена со всей области. Теперь в неё можно будет вводить любые данные.

По данным портала ЗАЧЕСТНЫЙБИЗНЕСМУНИЦИПАЛЬНОЕ КАЗЕННОЕ УЧРЕЖДЕНИЕ «УПРАВЛЕНИЕ КАПИТАЛЬНОГО СТРОИТЕЛЬСТВА МУНИЦИПАЛЬНОГО ОБРАЗОВАНИЯ БРЮХОВЕЦКИЙ РАЙОН»По данным портала ЗАЧЕСТНЫЙБИЗНЕС2327013058

О компании:
МКУ «УКС МОБР» ИНН 2327013058, ОГРН 1132363000175 зарегистрировано 12.03.2013 в регионе Краснодарский Край по адресу: 352750, Краснодарский кр, станица Брюховецкая, район Брюховецкий, улица Красная, 211. Статус: Действующее. Размер Уставного Капитала — руб.

Руководителем организации является: Начальник — Бандуров Виталий Григорьевич, ИНН . У организации 1 Учредитель. Основным направлением деятельности является «деятельность в области архитектуры, инженерных изысканий и предоставление технических консультаций в этих областях».

Рейтинг организации:
Высокий
  подробнее

ВНИМАНИЕ: для оценки рисков работы с данной организацией рекомендуем отчет

Должная осмотрительность ?

Статус: ?
Действующее

Дата регистрации: По данным портала ЗАЧЕСТНЫЙБИЗНЕС

?
По данным портала ЗАЧЕСТНЫЙБИЗНЕС

12.03.2013
Размещенные вакансии

ОГРН  ?	1132363000175    присвоен: 12.03.2013
ИНН  ?	2327013058
КПП  ?	232701001
ОКПО  ?	10122371
ОКТМО  ?	03610407101

Реквизиты для договора 
?
 …Скачать

Проверить блокировку cчетов 
?

Контактная информация +7(8… Посмотреть
?

Отзывы об организации 
?: 0   Написать отзыв

Юридический адрес: ?
По данным портала ЗАЧЕСТНЫЙБИЗНЕС
352750, Краснодарский кр, станица Брюховецкая, район Брюховецкий, улица Красная, 211
получен 04.03.2016
зарегистрировано по данному адресу:
По данным портала ЗАЧЕСТНЫЙБИЗНЕС

По данным портала ЗАЧЕСТНЫЙБИЗНЕС
Руководитель Юридического Лица ?По данным портала ЗАЧЕСТНЫЙБИЗНЕС
НачальникПо данным портала ЗАЧЕСТНЫЙБИЗНЕС

Бандуров Виталий Григорьевич

ИНН ?	По данным портала ЗАЧЕСТНЫЙБИЗНЕС
действует с	По данным портала ЗАЧЕСТНЫЙБИЗНЕС 09.06.2018

Учредители ? ()

По данным портала ЗАЧЕСТНЫЙБИЗНЕС По данным портала ЗАЧЕСТНЫЙБИЗНЕС АДМИНИСТРАЦИЯ МУНИЦИПАЛЬНОГО ОБРАЗОВАНИЯ БРЮХОВЕЦКИЙ РАЙОН По данным портала ЗАЧЕСТНЫЙБИЗНЕС 12.03.2013 , ИНН

Основной вид деятельности: ?По данным портала ЗАЧЕСТНЫЙБИЗНЕС
71.1 деятельность в области архитектуры, инженерных изысканий и предоставление технических консультаций в этих областях

Дополнительные виды деятельности:

Единый Реестр Проверок (Ген. Прокуратуры РФ) ?

Реестр недобросовестных поставщиков: ?
По данным портала ЗАЧЕСТНЫЙБИЗНЕС

не числится.

Реестр операторов, осуществляющих обработку персональных данных (Данные РКН) ?

Регистрационный номер:	По данным портала ЗАЧЕСТНЫЙБИЗНЕС 23-16-006129 от По данным портала ЗАЧЕСТНЫЙБИЗНЕС 17.10.2016
Дата начала обработки:	По данным портала ЗАЧЕСТНЫЙБИЗНЕС 25.02.2013

Налоговый орган ?
По данным портала ЗАЧЕСТНЫЙБИЗНЕС
Межрайонная Инспекция Федеральной Налоговой Службы № 4 По Краснодарскому Краю
Дата постановки на учет: По данным портала ЗАЧЕСТНЫЙБИЗНЕС
12.03.2013

Регистрация во внебюджетных фондах

Фонд	Рег. номер	Дата регистрации
ПФР  ?	033029023103	По данным портала ЗАЧЕСТНЫЙБИЗНЕС 21.03.2013
ФСС  ?	231242287123121	По данным портала ЗАЧЕСТНЫЙБИЗНЕС 14.03.2013

Коды статистики

ОКАТО  ?	03210807001
ОКОГУ  ?	4210007
ОКОПФ  ?	75404
ОКФС  ?	14

Финансовая отчетность МКУ «УКС МОБР» ?

В качестве Поставщика: , на сумму

В качестве Заказчика: , на сумму

По данным портала ЗАЧЕСТНЫЙБИЗНЕС

Судебные дела МКУ «УКС МОБР» ?

найдено по ИНН: По данным портала ЗАЧЕСТНЫЙБИЗНЕС

найдено по наименованию (возможны совпадения): По данным портала ЗАЧЕСТНЫЙБИЗНЕС

По данным портала ЗАЧЕСТНЫЙБИЗНЕС

Исполнительные производства МКУ «УКС МОБР»
?

найдено по наименованию и адресу (возможны совпадения): По данным портала ЗАЧЕСТНЫЙБИЗНЕС

По данным портала ЗАЧЕСТНЫЙБИЗНЕС

Лента изменений МКУ «УКС МОБР»
?

Не является участником проекта ЗАЧЕСТНЫЙБИЗНЕС ?

Больше информации об организации — в Премиум доступе

2.8. Критическая ошибка в Excel 2003

В Excel 2003 функции TREND и
LINEST при определенных
условиях дают неверный результат.

Так происходит когда одновременно:

• среднее значение по каждой переменной в матрице
  предикторов X равно нулю;

• среднее значение отклика Y
  не равно нулю.

На показан как раз такой
случай: средние значения по всем столбцам матрицы Xc
равны нулю, а среднее по столбцу Yc отлично от нуля..

Пример 
 

Рис.37 Ошибка в регрессионных функциях Excel
2003

Ситуацию можно исправить, применяя функцию
TREND к
центрированным значениям отклика, с последующей коррекцией результата.
Для этого можно использовать формулу
=TREND(Yc-ym,
Xc)+ym, применение которой показано на том же рисунке.

Удивительно, но эта ошибка не была замечена
пользователями. Однако в новой версии 2007 она исправлена.  

Виды массивов функций в Excel

В целом, можно перечислить следующие виды массивов функций в Excel:

1. Одномерные. Их характерная особенность заключается в том, что они включают только ячейки одного ряда или колонки.
2. Двумерные массивы могут содержать огромное количество ячеек как в пределах ячеек или колонок одного листа, так и нескольких.

Таким образом, массивы функций дают возможность обрабатывать огромное количество данных, состоящих из сотен и даже тысяч ячеек. Причем даже тех, которые находятся за пределами листа.

2

В свою очередь, одномерные массивы можно разделить на горизонтальные и вертикальные. Первые включают ячейки одного ряда, а вторые – колонки.

Формулы массива позволяют обрабатывать информацию из всего разнообразия данных.

Синтаксис формулы массива

Давайте представим, что у нас есть таблица, в которой есть набор ячеек, а сумма к оплате описывается в одной ячейке. Для первого будем искать промежуточные итоги. Во втором же случае будем рассчитывать итоговую сумму.

Для начала нам нужно выделить диапазон, к какому в дальнейшем будет применена формула. В нашем случае это набор ячеек, начинающийся E3, а заканчивающийся E8.

Затем ставим курсор в строку формул, и там записываем =C3:C8*D3:D8.

3

Превращаем формулу в формат массива. Нужно нажать Ctrl + Shift + Enter.

После этого мы получаем таблицу с готовыми промежуточными итогами.

4

Как видим, после совершения этих операций формула облачилась в фигурные скобки. Именно они и говорят о том, что эта функция будет обрабатываться, как формула массива. Видим, что каждая ячейка каждого ряда превратилась в готовый результат. 

Если попробовать внести какие-угодно изменения в результирующую ячейку, то появится такое уведомление о том, что операция запрещена.

5

Давайте приведем еще один вариант использования формулы массива. На этот раз мы выведем только одно результирующее значение в итоговую ячейку. Чтобы достичь этой цели, необходимо выполнить следующие действия.

1. Выделяем ту ячейку, которая будет содержать результат вычисления по формуле массива.
2. Вводим туда формулу. В нашем случае мы будем суммировать значения из целевого диапазона, поэтому используем формулу СУММ(C3:C8*D3:D8).
3. С использованием комбинации Ctrl + Shift + Enter осуществляем трансформацию стандартной формулы в ту, которая работает с массивами данных.

По итогу, получаем следующий результат.

6

В случае, если бы мы не знали, как правильно использовать формулы массива, нам бы пришлось использовать две обычные. А так мы избавлены от этой необходимости. 

Давайте более подробно рассмотрим синтаксис этой формулы. 

В нашем случае были использованы одномерные массивы. Формула обрабатывает каждый, после чего выполняет необходимые результаты, а итог выводит в ячейку.

Составные части формул массива:

1. Функция массива. Это описание той операции, которую Эксель должен выполнить. 
2. Массивы диапазона. Это непосредственно те диапазоны, которые будут обрабатываться формулой. 
3. Оператор массива – знак двоеточия. Обозначает расстояние в определенное количество ячеек между конкретными адресами. 

Чтобы было проще понять, вот небольшой рисунок.

7

2.7. Регрессия

Для построения используются
несколько стандартных функций листа.

TREND / ТЕНДЕНЦИЯ

Строит

y=b+m₁x₁+…+m_J x_J+e

Аппроксимирует известные значения вектора откликов
known_y’s для заданных значений матрицы предикторов
known_x’s и возвращает значения y,
для заданного массива new_x’s.  

Синтаксис 

TREND(known_y’s
)

Примечания 

• Вектор
  known_y’s должен занимать один столбец,
  тогда каждый столбец матрицы массива known_x’s
  интерпретируется как отдельная переменная;

• Если
  аргумент known_x’sопущен, то предполагается, что это вектор чисел {1;2;3;…}
  такого же размера, как и known_y’s;

• Матрица
  новых значений new_x’sдолжна иметь столько же столбцов
  (переменных), как и матрица known_x’s;

• Если
  аргумент new_x’sопущен, то предполагается, что он совпадает с
  массивом known_x’s.
  Результат является вектором, в котором число строк равно
  числу строк в массиве new_x’s.

Пример 
 

Рис.34 Функция TREND

Функция TRENDявляется функцией
массива и ее ввод должен завершаться нажатием комбинации
CTRL+SHIFT+ENTER. 

LINEST /
ЛИНЕЙН

Дополняет функцию TREND и выводит некоторые
статистические значения, связанные с регрессией  

y=b+m₁x₁+…+m_J x_J+e

Синтаксис 

LINEST(known_y’s
)

Рис. 35 Таблица вывода функция LINEST

m_J, …,
m₂, m₁
и b – оценки регрессионных
коэффициентов;

s_J, …,
s₂, s₁
и s_b
– стандартные ошибки для оценок регрессионных коэффициентов;

R2 –
коэффициент детерминации;

s_y –
стандартная ошибка оценки y;

F – F-статистика;

DoF – число степеней
свободы;

SS_reg –
регрессионная сумма квадратов;

SS_res–
остаточная сумма квадратов.

Примечания 

• LINEST – это
  очень плохо сконструированная функция, очень неудобная в
  практическом применении;

• Примечания,
  представленные в описании функции полностью применимы к
  функции LINEST.

Пример 
 

Рис.36 Функция LINEST

Функция LINEST является функцией массива и ее ввод должен
завершаться нажатием комбинации CTRL+SHIFT+ENTER. 

Изменение содержимого массива

Новички нередко сталкиваются с трудностями в попытках изменить часть массива, потому что каким бы способом они не пытались бы выкрутиться, Эксель все равно показывает сообщение, что это сделать нельзя. Тем не менее, все гениальное просто. В этом случае – также. Достаточно просто выполнить несколько элементарных действий:

1. Найти кнопку «Отмена», расположенную слева от строки формул. Еще один вариант – нажатие клавиши Esc, которая выполняет ту же операцию. Во всех случаях блокировка будет снята и все операции можно выполнять заново. 
2. Снова ввести формулу массива с тем же диапазоном.

Таким образом, изменение содержимого массива возможно лишь если все отменить, а потом заново вводить формулу. Неудобно, конечно, но значительно удобнее, чем использовать стандартные формулы.