Арабские цифры и числительные в египетском языке
Содержание:
- Первый опыт с вертикальной мышью
- Происхождение системы
- История появления арабских цифр
- Часть 3. Реконструкция событий.
- Латинские (римские) цифры
- Пишем на клавиатуре
- Часть 2. Преобразование буква — цифра.
- Сервисы по преобразованию арабских цифр в римские
- История появления римских цифр
- Формирование римских цифр – счёт от 1 до 100
- Часть 1. Теория.
- Использование нуля в расчетах
Первый опыт с вертикальной мышью
Несмотря на все вышеописанное и появление первых симптомов туннельного синдрома, я долго не решался сменить мышь.
В качестве первой попытки была взята безымянная китайская Delux M618 — после игровой Xiaomi и множества Logitech выбор кажется странным.
Увы, в бюджетном и среднем сегменте найти что-то лучше маловероятно: существуют разнообразные проводные и беспроводные Delux, пара DNS (тоже самое), изредка попадаются Trust.
Logitech венчают список, стартуя от 6 тысяч. К тому же, в моем городе её можно купить только под заказ без возможности распаковки на месте и возврата.
Поэтому и был выбран беспроводной 3-кнопочный Delux. Не самый плохой бренд, пусть и с некоторым «душком». От китайской мышки многого ждать не приходится.
Дешёвая, простая, совершенно дубовая — пластик паршивенький. Кликает громко, но приятно. Хотя все это сейчас не имеет никакого значения.
Происхождение системы
Система тесно связана с древним городом-государством Римом и созданной им Империей. Однако из-за нехватки сохранившихся примеров происхождение системы неясно, и существует несколько конкурирующих теорий, все в значительной степени предположительные.
Этрусские цифры
Рим был основан где-то между 850 и 750 годами до нашей эры. В то время этот регион был населен разнообразным населением, наиболее развитым из которых были этруски. Сами древние римляне признавали, что основу большей части их цивилизации составляли этруски. Сам Рим был расположен рядом с южной окраиной этрусских владений, которые занимали большую часть северо-центральной Италии.
Римские цифры, в частности, являются прямым производным от этрусских цифровых символов : «» »,« ? »,« ? »,« ? »и« ? »для 1, 5, 10, 50 и 100 (у них больше символов для больших чисел, но неизвестно, какой символ представляет какое число). Как и в основной римской системе, этруски писали символы, которые добавляли к желаемому числу, от большего к меньшему значению. Таким образом, число 87, например, будет записано 50 + 10 + 10 + 10 + 5 + 1 + 1 = ??????? (это будет отображаться как ???????, поскольку этрусский писался справа налево).
Символы «?» и «?» напоминали буквы этрусского алфавита, а «?», «?» и «?» — нет. Этруски тоже использовали субтрактивную нотацию, но не так, как римляне. Они написали 17, 18 и 19 как «?????», «????» и ???, отражая то, как они произносили эти числа («три из двадцати» и т. Д.); и аналогично для 27, 28, 29, 37, 38 и т. д. Однако они не писали «??» вместо 4 (или «??» для 40), а писали «???», «????» и «?????» вместо 7, 8 и 9 соответственно.
Ранние римские цифры
Ранние римские цифры для 1, 10 и 100 были этрусскими: « I », « X » и « Ж ». Символы 5 и 50 в какой-то момент изменились с Ʌ и «?» на V и ↆ. Последнее было уплощенная ⊥ (перевернутой буквы Т) ко времени Августа , и вскоре после этого стал отождествляться с графически аналогичной буквой L .
Символ для 100 записывался по-разному как > I < или ƆIC , затем был сокращен до Ɔ или C , при этом C (которая соответствовала латинской букве), наконец, выиграла. Возможно, помогло то, что C — это начало слова centum , латинское слово «сотня».
Числа 500 и 1000 были обозначены буквами V или X, наложенными прямоугольником или кружком. Таким образом, 500 было похоже на Ɔ, наложенное на Þ . Это стало D или Ð ко времени Августа, под влиянием графического письма D . Позже она была идентифицирована как буква D ; альтернативный символ «тысяча» был CIƆ , и половины из тысячи или «пятьсот» является правой половина символа, IƆ , и это , возможно, было преобразовано в D .
Обозначение для 1000 представляло собой обведенный или заключенный в квадрат X : Ⓧ, ⊗ , ⊕ , а во времена Августина частично отождествлялся с греческой буквой Φ phi . Со временем символ изменился на Ψ и ↀ . Последний символ в дальнейшем превратилось в ∞ , то ⋈ , и в конечном счете изменены на М под влиянием латинского слова промилле «тысячи».
По словам Пола Кайзера, основными числовыми символами были I , X , C и Φ (или ⊕ ), а промежуточные были получены путем взятия половины из них (половина X — это V , половина C — это L, а половина — Φ / ⊕. это D ).
Вход в секцию LII (52) Колизея , цифры все еще видны.
Классические римские цифры
Колизей был построен в Риме в CE 72-80, и в то время как оригинальные стены по периметру в основном исчезла, пронумерованный от входа XXIII (23) LIIII (54) выживает, чтобы продемонстрировать , что в имперские времена римских цифр уже считать их классическими форма: . Самая очевидная аномалия ( ) — это непоследовательное использование вычитающей записи: в то время как XL используется для 40, IV избегается в пользу IIII : фактически вентиль 44 обозначен как XLIIII .
История появления арабских цифр
Арабские числовые знаки были выдуманы и записаны в Индии, произошло это около 5 века. В это время был определен отсчет чисел при перечислении. Отправной точкой был ноль (оригинальное название шунья). Это число позволило сформировать нынешний порядок чисел при счете. Популяризацией арабских цифр занимался индийский ученый того времени Абу Аль-Хорезми, который создал несколько книг на эту тему. От одной из них произошло сегодняшнее название школьного предмета — алгебра. Предоставленный ученым способ записи числовых значений использовал десятичную систему.
Археологи находили разные работы древних математиков и археологов, которые использовали арабские цифры для своих работ. Эти работы были созданы предположительно в 8-9 веке. Сегодня большинство арабских стран используют отличительную от привычной всем записи чисел в европейских и других регионах. Более того, на Востоке принято писать порядок чисел с права налево.
Существует множество мнений, что в формировании цифр арабского происхождения, которыми пользуемся сегодня мы — 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, были использованы не только арабские цифры древней Индии. Посмотрев на таблицу арабских цифр в диапазоне от 1 до 10 старого и нового представления, можно найти множество сходств. Например, 1, 2, 3, 4 в начальном представлении — это те же знаки, только повернутые на 90 градусов.
Часть 3. Реконструкция событий.
Давным-давно наши предки решили основательно упорядочить свою жизнь. С этой целью они придумали календарь. По причине того, что периоды Луны были более короткими, а значит, легче заметными, чем солнечные. Поэтому, первым был создан лунный календарь, в котором 27 дней каждого месяца были разделёны на три периода (три недели) по 9 дней. В русских сказках эта информация сохранилась в виде слов: «у отца было три сына» (у месяца три периода), «тридевятое царство», «за тридевять земель». Да и умерших поминали на девятый день. Это очень удобно – не надо считать дни. Если в пятницу умер, то ровно через неделю, в следующую пятницу, поминают.
Действительно, славянская неделя состояла из девяти дней:
| 1. | ПонедЕльник. |
| 2. | ВтОрник. |
| 3. | ТретЕйник. |
| 4. | ЧетвЕрик. |
| 5. | ПятнИца. |
| 6. | ШестИца. |
| 7. | СедьмИца. |
| 8. | ОсьмИца. |
| 9. | НедЕля. |
Последний – девятый – день был выходным, когда ничего не делали. Потому он и назван «неделя». Здесь всё понятно. Но почему первый день недели назван не первиком или, к примеру, первейником? Ответ напрашивается сам собой: потому, что один или единица – это фаллический символ бога, его имя. А имя бога нельзя произносить в быту (в суе). Оно было тайным. Пришлось скрыть истинное название, и первый день назвали понедельником – тот, который после недели, после выходного дня.
Как мы видим, числа в те времена уже были или только начинали создаваться, но цифр ещё не было. Предполагается также, что письменность уже существовала. Естественно, что со временем встал вопрос обозначения чисел при письме.
Как бы то ни было, но именно эти девять дней, точнее – девять цифр, им соответствующих – легли в основу первой, древней системы счисления. Со временем, после изобретения ноля, эта система стала десятичной. И десять пальцев на руках не имеют к этой системе никакого отношения. Это просто совпадение.
Telecar.
24 июня 2014 г.
Латинские (римские) цифры
Для обозначения цифр в латинском языке приняты комбинации следующих семи знаков: 1(1), V(5), X(10), L(50), С(100), D(500), M(1000). Если знак, обозначающий меньшее число, стоит справа от знака, обозначающего большее число, то меньшее число следует прибавлять к большему, если — слева, то вычитать, а именно:
- VI — 6, т. е. 5+1
- IV — 4, т. е. 5-1
- XI — 11, т. е. 10+1
- IX — 9, т. е. 10-1
- LX — 60, т. е. 50+10
- XL — 40, т. е. 50-10
- СХ — 110, т. е. 100+10
- ХС — 90, т. е. 100-10
- MDCCCXII — 1812, т. е. 1000+500+100+100+100+10+1+1
- MCMXVII — 1917, т. е. 1000+1000-100+10+5+1+1
- MCMLXI — 1961, т. е. 1000+1000-100+50+10+1
Ниже представлены латинские цифры, их текстовое написание и русское произношение:
- I (1) — unus .
- II (2) — duo .
- III (3) — tres .
- IV (4) — quattuor .
- V (5) — quinque .
- VI (6) — sex .
- VII (7) — septem .
- VIII (8) — octo .
- IX (9) — novem .
- X (10) — decem .
- XI (11) — undecim .
- II (12) — duodecim .
- XIII (13) — tredecim .
- XIV (14) — quattuordecim .
- XV (15) — quindecim .
- XVI (16) — sedecim .
- XVII (17) — septendecim .
- XVIII (18) — duodeviginti .
- XIX (19) — undeviginti .
- XX (20) — viqinti .
- XXI (21) — unus et viginti или viginti unus.
- XXII (22) — duo et viginti или viginti duo
- и т. д.
- XXVIII (28) — duodetriginta .
- XXIX (29) — undetriginta .
- XXX (30) — triginta .
- XL (40) — quadraginta .
- L (50) — quinquaginta .
- LX (60) — sexaginta .
- LXX (70) — septuaginta .
- LXXX (80) — octoginta .
- XC (90) — nonaginta .
- С (100) — centum .
- CC (200) — ducenti .
- CCC (300) — trecenti .
- CD (CCCC) (400) — quadringenti .
- D (500) — quingenti .
- DC (600) — sescenti или sexcenti .
- DCC (700) — septingenti .
- DCCC (800) — octingenti .
- CM (DCCCC) (900) — nongenti .
- M (1000) — mille .
- ММ (2000) — duo milia .
- V (5000) — quinque milia .
- X (10000) — decem milia .
- XX (20000) — viginti milia .
- С (100000) — centum milia .
- XI (1000000) — decies centena milia .
Римляне, как известно, использовали для записи числа латинские буквы. Считается, что римская система счисления является классическим примером непозиционной системы счисления, то есть такой системы счисления, в которой величина, которую обозначает цифра, не зависит от положения в числе. Напомним, что в римской системе счисления I обозначает 1, V обозначает 5, X — 10, L — 50, C — 100, D — 500, M — 1000. Например, число 3 в римской системе счисления будет обозначаться как III.
Однако на самом деле не все так просто, и она не является полностью непозиционной системой счисления, потому что в римской системе счисления есть дополнительное правило, которое влияет на величину, которую обозначает цифра, в зависимости от ее положения. Правило это запрещает употреблении одной и той же цифры более 3 раз подряд, поэтому три это III, а четыре это уже IV, и I(1), стоящая перед большей цифрой V(5), обозначает вычитание, то есть фактически равна -1.
Ниже два калькулятора — для перевода числа из диапазона 1 – 3999 в римское число и наоборот. Для чисел больше 3999 используется несколько другая нотация.
Пишем на клавиатуре
Практически все документы, дипломные работы, книги пишутся сейчас на компьютерах. В связи с этим возникает необходимость написания римских знаков на клавиатуре. На самом деле сделать это просто – можно пользоваться символами латинского алфавита. Стандартный вариант набора:
- переключаем клавиатуру на английский язык;
- нажимаем кнопку CapsLock , ведь римские значения пишутся верхним регистром латинской системы алфавита.
Если необходимо ввести длинную комбинацию, к примеру, 177, то для начала проводится вычисление: 100+70+7. После этого набираете с большего числа – CLXXVII. При написании очень больших цифр появляются сложности, в таком случае можно воспользоваться специальными числовыми конвертерами. Подобные онлайн сервисы можно поискать в сети, в свободном доступе есть и картинки с правильным обозначением.
Кроме того, для ввода цифр из Древнего Рима на компьютерных устройствах часто применяются специализированные ASCII коды, для их включения нужно — активировать режим Num Lock , затем, удерживая Alt , ввести определенное сочетание в дополнительной клавиатуре:
- Alt +73 – I;
- Alt +86 – V;
- Alt +88 – X;
- Alt +76 – L;
- Alt +67 – C;
- Alt +68 – D;
- Alt +77 – M.
Данный вариант на первый взгляд кажется сложным, но если работать с таблицей часто, можно быстро понять.
Автор рекомендует:
- Как поставить в Ворде ударение над буквой
- WPS Office — что это за программа, стоит ли её устанавливать?
- Как найти фотографию в интернете по фотографии
- Где найти и как запустить калькулятор на Windows 7/8/10: все способы
- Исправляем ошибку при направлении команды приложению Excel
Часть 2. Преобразование буква — цифра.
ОДИН. Что такое «одИн»? Если изменить ударение, то получится «Один» — древнегерманский языческий бог. Самый главный из всех богов. Бог №1.
Также, если возьмём слово «единица», то убрав первую букву, получим «Денница» — одно из имён Дьявола. Но это, конечно, случайное совпадение.
Как бы то ни было, мы можем предположить, что единица изначально имела мистический, религиозный смысл. Поэтому её начертание старались сохранять. К тому же мы не должны забывать, что «римские цифры» появились раньше, чем современные «арабские». Следовательно, можно предположить, что современная цифра «1» произошла от «римской» цифры «I»:
Приведём несколько высказываний Блаватской из её «Тайной доктрины» в отношении скрытого смысла символа единицы:
ДВА. В своей статье Фоменко в качестве доказательства приводит фото фрагментов старых текстов:
Также он очень аргументировано и достаточно убедительно утверждает, что «в русском почерке конца XVIII века цифра «2» и буква «Д» писались одинаково. Вероятно потому, что «д» — это первая буква слова «два». Полное тождество буквы «д» и цифры «2» в почерке того времени очевидно, например, из надписи на другом рисунке XVIII века, который мы приводим…»
Предположим, что это действительно было так — букву Д и цифру 2 иногда или часто заменяли или путали. Заменять могли ради красоты почерка. Ведь, согласитесь, цифра «2» на приведённых фото выглядит очень эффектно. Но из этих рассуждений совершенно не ясно, что из чего произошло. Что первично и что вторично? Лично мне представляется более вероятным, что цифры произошли из букв, а не наоборот.
или
Если это так, тогда рассмотрим другие цифры.
ТРИ. Первую букву этого слова можно превратить в цифру, если положить её на бок. При этом не будем забывать про старое изображение этой буквы.
ЧЕТЫРЕ. Первая буква этого слова настолько сильно совпадает с цифрой «Ч», что нашим предкам пришлось создать вариант написания этой цифры в виде «4». Однако это сделано только в печатных изданиях. А от руки мы продолжаем писать четвёрку в виде буквы «Ч».
ПЯТЬ. Первую букву этого слова можно преобразовать в цифру «5» разными способами. Например, если взять две буквы «П» и соединить их валетом, то мы получим вполне современное изображение пятёрки:
хотя мне представляется более вероятным другой вариант её создания:
ШЕСТЬ. Опять смотрим на первую букву и делаем из неё цифру «6», положив букву «Ш» на бок. Нужно заметить, что это только один из вариантов.
СЕМЬ. Современная цифра «7» совершенно не похожа на первую букву — «С». Но, если мы посмотрим на рисунок, то станет понятно, что эта цифра раньше писалась иначе.
Давайте и мы опустим традиционную перемычку в самый низ.
Наша семёрка превратилась в букву Z.
Теперь, чтобы хоть немного оживить описание, приведу пример из художественного фильма «Азазель». Повествование этого фильма разделено на главы. Третья глава названа «Зутулый штудент».
«Штудент» — потому что штудирует. А вот почему «зутулый», а не сутулый? Попробую предположить: раньше так говорили. Возможно, что так говорили не везде; возможно, что это был локальный говор. Но со временем звонкая «З» была заменена на глухую «С». Было «земь», стало «семь». Произношение изменилось, а цифра осталась прежней. Вот почему цифру «7» делали из буквы «Z». Это старое обозначение современной буквы «З».
Теперь нужно отметить, что процесс преобразования буквенных знаков в цифровые проходил не сразу. Вероятно, что у него даже не было единого плана. Поэтому, можно утверждать, что этот процесс до сих пор не закончен. Например, цифру «7» уже многие начинают писать без средней горизонтальной черты.
ВОСЕМЬ. Здесь совсем просто: первая буква этого слова — «В» — абсолютно похожа на цифру «8».
ДЕВЯТЬ. Здесь первая буква «Д». Но ведь эта буква уже была использована при создании двойки. К сожалению, это так. Но как же наши предки выкрутились? А вот как – из одной буквы «Д» были созданы две разные цифры «2» и «9».
или
Сервисы по преобразованию арабских цифр в римские
Пользователям достаточно сложно запомнить все римские цифры от 1 до 100 и более. Тем более принципы их образования. Этого делать и не нужно. Есть специальные конвертеры, которые помогут вам преобразовать любые арабские цифры в римские и обратно. Одним из таких сервисов является calc.ru. Здесь вы сможете перевести арабские, римские или индийские цифры в разной последовательности. Переводить можно только целые числа.
Итак:
- Перейдите на страницу https://www.calc.ru/rimskiye-indiyskiye-arabskiye-tsifri.html.
- В поле «Перевести целое число» введите число, которое нужно перевести.
- Выберите одну из числовых систем мышью.
- Нажмите кнопку ниже «Перевести».
Под формой ввода находятся примеры записи веков римским цифрами.
Еще один удобный сервис для перевода любого арабского числа в римское. Здесь есть 2 поля ввода. Он находится по адресу http://infofaq.ru/perevod-v-rimskie-chisla.html.
Пользоваться им также достаточно просто:
- под описанием истории появления римских цифр, найдите форму;
- в первой строке можно вводить арабские цифры, в поле ниже отображается результат;
- и наоборот, если ввести в нижнее поле римскую цифру, вы получите результат в верхней строке.
История появления римских цифр
Интересным является тот факт, что эти необычные цифры дошли до наших времен не из-за каких-либо оригинальных или полезных свойств. А именно из-за большого влияния римлян и Римской империи в прошлом. Даже когда в 7 веке до нашей эры этруски завоевали Рим, им пришлось почувствовать влияние средиземноморских культур на себе. Об этом можно судить исходя из того, что в их культуре сразу же произошли изменения, которые касаются в первую очередь представлением цифр в письме. После этих событий обе системы имели множество схожих элементов в числах.
В многих древних рукописях цифра пять (5) представлена в одном и том же виде — V. Но её достоверное происхождение не определено и по сей день. Одни историки утверждают, что знак символизирует раскрытую ладонь с прижатыми четырьмя пальцами и оттопыренным большим пальцем. Множество споров вызвала римская цифра десять (10) — X. Её происхождение также связывают с человеческими конечностями — руками. Римская «десятка» символизирует скрещенные руки. Таким образом, во многих отраслях производства (например, в строительстве) римляне могли показать друг другу числовые значения, используя руки.
До сих пор не установлен источник возникновения римских цифровых знаков. Но были замечены заимствования элементов символов из других народов. Например, римские цифры сто и тысяча похожи на некоторые древнегреческие буквы. Известно также, что римляне не были склонны и заинтересованы в глубоких познаниях математики. Поэтому их представление максимального числа сегодня выглядит смешным — 399 999. Дробных представлений чисел римляне вовсе избегали. Иногда, если это было слишком необходимо, определенную единицу измерения делили на 12. Сегодня такой прием также используется, когда мы выражаем длину в футах, дюймах и пр.
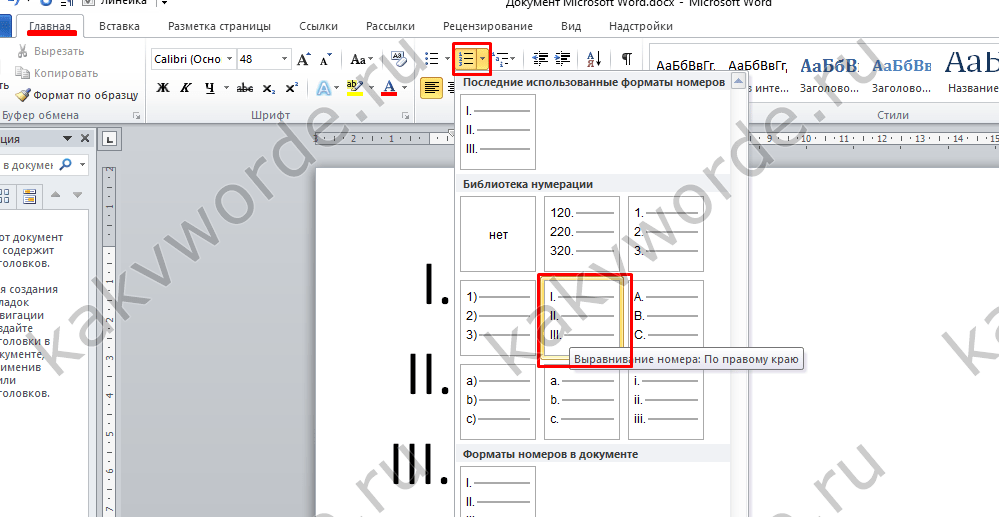
Формирование римских цифр – счёт от 1 до 100
До 19 века число 4 на римский манер записывалось как IIII. Затем число изменили, и оно обрело новый, упрощенный вид — IV (5 — 1). Меньшие цифры могут стоять перед большими. В этом случае они отнимаются от большего. И наоборот, если единицы стоят после десятков, то они суммируются, например, VI (5 + 1) — это цифра 6. При этом вычесть можно только цифру, обозначающую один или степени десятки. Уменьшаемые могут быть только ближайшие к вычитаемому в числовом ряду две цифры.Нельзя повторять меньшие цифры в числе.
Из этого следует только 6 примеров правила вычитания:
- CM (1 000 — 100) — 900;
- CD (500 — 100) — 400;
- XC (100 — 10) — 90;
- IX (10 — 1) — 9;
- IV (5 — 1) — 4.
Например, число 94 римскими цифрами будет XCIV, то есть: 100 — 10 + 5 — 1. Стоить заметить, что другие методы вычитания применять ранее было недопустимо. Запись арабской цифры 99 должно выглядеть так: XCIX, а не IC. Но в наши дни в популярном текстовом редакторе Microsoft Word и Microsoft Excel применяются упрощенные числа. Здесь допустимо использоваться конструкцию IC, а также другие — VC (95), вместо XCV и так далее.
Некоторые фирмы по производству часов до сих пор используют запись четверки как IIII. Скорее всего делают они это скорее по эстетическим соображениям. Есть несколько версий о том, почему такая форма более приемлема.
По одной из версий запись IV является в имени бога дневного света и неба Юпитера первой буквой — IVPITER.
|
Арабские цифры: |
Римские цифры: |
|---|---|
|
1 |
I |
|
2 |
II |
|
3 |
III |
|
4 |
IV |
|
5 |
V |
|
6 |
VI |
|
7 |
VII |
|
8 |
VIII |
|
9 |
IX |
|
10 |
X |
|
11 |
XI |
|
12 |
XII |
|
13 |
XIII |
|
14 |
XIV |
|
15 |
XV |
|
16 |
XVI |
|
17 |
XVII |
|
18 |
XVIII |
|
19 |
XIX |
|
20 |
XX |
|
21 |
XXI |
|
22 |
XXII |
|
23 |
XXIII |
|
24 |
XXIV |
|
25 |
XXV |
|
26 |
XXVI |
|
27 |
XXVII |
|
28 |
XXVIII |
|
29 |
XXIX |
|
30 |
XXX |
|
31 |
XXXI |
|
32 |
XXXII |
|
33 |
XXXIII |
|
34 |
XXXIV |
|
35 |
XXXV |
|
36 |
XXXVI |
|
37 |
XXXVII |
|
38 |
XXXVIII |
|
39 |
XXXIX |
|
40 |
XL |
|
41 |
XLI |
|
42 |
XLII |
|
43 |
XLIII |
|
44 |
XLIV |
|
45 |
XLV |
|
46 |
XLVI |
|
47 |
XLVII |
|
48 |
XLVIII |
|
49 |
XLIX |
|
50 |
L |
|
51 |
LI |
|
52 |
LII |
|
53 |
LIII |
|
54 |
LIV |
|
55 |
LV |
|
56 |
LVI |
|
57 |
LVII |
|
58 |
LVIII |
|
59 |
LIX |
|
60 |
LX |
|
61 |
LXI |
|
62 |
LXII |
|
63 |
LXIII |
|
64 |
LXIV |
|
65 |
LXV |
|
66 |
LXVI |
|
67 |
LXVII |
|
68 |
LXVIII |
|
69 |
LXIX |
|
70 |
LXX |
|
71 |
LXXI |
|
72 |
LXXII |
|
73 |
LXXIII |
|
74 |
LXXIV |
|
75 |
LXXV |
|
76 |
LXXVI |
|
77 |
LXXVII |
|
78 |
LXXVIII |
|
79 |
LXXIX |
|
80 |
LXXX |
|
81 |
LXXXI |
|
82 |
LXXXII |
|
83 |
LXXXIII |
|
84 |
LXXXIV |
|
85 |
LXXXV |
|
86 |
LXXXVI |
|
87 |
LXXXVII |
|
88 |
LXXXVIII |
|
89 |
LXXXIX |
|
90 |
XC |
|
91 |
XCI |
|
92 |
XCII |
|
93 |
XCIII |
|
94 |
XCIV |
|
95 |
XCV |
|
96 |
XCVI |
|
97 |
XCVII |
|
98 |
XCVIII |
|
99 |
XCIX |
|
100 |
C |
|
101 |
CI |
Часть 1. Теория.
Общеизвестна теория, описывающая возможный способ создания арабских цифр. Согласно ей каждая цифра содержит в своём написании соответствующее количество углов: цифра один содержит в своём написании один угол, цифра два содержит два угла и т.д. до девятки, которая содержит соответственно девять углов.
Некоторые исследователи полагают, что именно такое соответствие углов (на рисунке выше) легло в основу написания современных цифр.
Однако, эта теория вызывает несколько вопросов. Почему двойка в данном исполнении больше похожа на семёрку, а семёрка на двойку?
Также у единицы изначально не было углов. Она изображалась как одна вертикальная черта. Это можно увидеть на картине Дюрера в магическом квадрате:
Ещё остаётся совершенно непонятным, почему эти цифры были названы арабскими. Нам известны настоящие арабские цифры, они показаны на рисунке в верхнем ряду:
Как мы видим, арабская вязь совершенно не соответствует форме написания современных цифр. То же можно сказать и про индийские, и про китайские, и про любые другие, якобы древние, цифры.
Я не буду утруждать читателей анализом всех теорий и фантазий о происхождении современных цифр и сразу перейду к делу. Моя теория заключается в том, что современные цифры были созданы
во-первых: из букв только русского алфавита,
во-вторых: из первой буквы русского названия каждой цифры (кроме единицы, тут случай особый).
Такой путь создания цифр объясняется тем, что из-за высокой цены пергамента некоторые писари сокращали текст до первой буквы каждого слова. Это общеизвестно. Но, чтобы не перепутать обычные слова с числами, пришлось как-то видоизменять те буквы, которые обозначали числа.
Использование нуля в расчетах
Детей в школе учат начинать отсчет с единицы. Но большинство программистов используют вычисления, где отсчет всегда начинается с нуля. Такая запись всех 10 чисел удобна тем, что для их представления используется только 1 символ. А экономия в программировании является неотъемлемой его частью. Если мы начнем отсчет с нуля, записывать цифру 10 нам не нужно. Её место занимает девятка.
Ноль обладает другими интересными свойствами при взаимодействии с числами. Так, если вы попытаетесь прибавить к нулю или отнять ноль от какого-нибудь числа — оно не изменится. Когда производится умножение на это число — вы получите 0 во всех случаях. При возведении каждого числа в ноль, получится единица. А также на ноль (0) нельзя разделить другое целое или дробное число.
Существует Закон Бенфорда. Если не вдаваться в подробности с рассмотрением формул и таблиц, он гласит, что в реальной жизни цифры от 1 до 4 встретить гораздо вероятнее, чем цифры от 5 до 9. Сюда можно отнести номера домов улиц, различную статистику и тому подобное. Есть у этого закона и практическое применение. Используя его, можно проверять бухгалтерские отчетности, результаты голосований, подсчет расходов.
В некоторых американских штатах несоответствие каких-либо расчетов по Закону Бенфорда является уликой, имеющей вес в судебном процессе. Все расчеты по этому закону производятся в десятичной системе. Таким образом, арабские цифры в границе от 1 до 10 являются самыми распространенными во всем мире.
https://youtube.com/watch?v=hMoN_Z23Upg